Ungedämpfte freie Schwingung
- Feder-Masse-System:
- Masse m an Feder mit Federkonstanten c
- als Applet zum Experimentieren
- Federkraft
- Ff = - c x (Hookesches Gesetz)
- Trägheitskraft
- Ft = - m
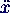
- Bewegungsgleichung
- Mit der Abkürzung
- erhält man
- Lösung der Bewegungsgleichung:
- lineare Dgl. mit konstanten
Koeffizienten
- Exponentialansatz
- Einsetzen in die Dgl. liefert Beziehung für ω
- 2 Lösungen für ω
- damit 2 Lösungen für x
- lineare Dgl. mit reellen Koeffizienten →
Realteil und Imaginärteil sind Lösung
- x1(t) = Re{xa} =
cos(ω0 t)
- x2(t) = Im{xa} =
sin(ω0 t)
- allgemeine Lösung ist Superposition von
x1 und x2
- x(t) = A cos(ω0 t) + B
sin(ω0 t)
- harmonische Schwingung mit Frequenz
- f = ω0/2π
(Eigenfrequenz)
- Anfangsbedingungen:
- bestimmen von A, B aus
- x(0) = x0
(Anfangsauslenkung)
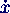 (0)
= v0 (Anfangsgeschwindigkeit)
(0)
= v0 (Anfangsgeschwindigkeit)
- Einsetzen in allgemeine Lösung →
- damit vollständige Lösung
- x(t) = x0 cos(ω0 t)
+ v0/ω0 sin(ω0
t)
- Bestimmung von Amplitude und Phasenverschiebung:
- Überlagerung von Kosinus- und Sinusschwingung ergibt
- x(t) =
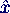 cos(ω0 t + φ)
cos(ω0 t + φ)
-
Formeln zur Addition harmonischer
Schwingungen liefern mit φ1 = 0, φ2 = -π/2
- Achtung: ggf. π zur Lösung von φ addieren!
- Aufgaben:



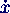 (0)
= v0 (Anfangsgeschwindigkeit)
(0)
= v0 (Anfangsgeschwindigkeit)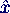 cos(ω0 t + φ)
cos(ω0 t + φ)