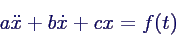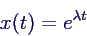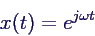Exkurs: Lineare Differentialgleichungen mit konstanten Koeffizienten

• Grundtyp der Gleichung 2. Ordnung:
  • für gesuchte Funktion x(t)
    • 
  • homogen ⇔ f(t) = 0
  • inhomogen ⇔ f(t) ≠ 0
• Lösungen der homogenen Gleichung:
  • in der Regel zu finden durch Exponentialansatz
    • wahlweise reell
    • 
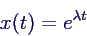
    • oder komplex
    • 
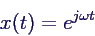
  • Linearkombination von Lösungen ist Lösung
  • komplexe Lösung ⇒ Realteil und Imaginärteil sind Lösungen (bei reellen Koeffizienten a, b, c)
  • Lösung hängt von 2 Parametern ab (Anfangsbedingungen!)
• Lösungen der inhomogenen Gleichung:
  • finde eine einzige Lösung x_spez(t) der inhomogenen Gleichung
  • Lösung der homogenen Gleichung sei x_hom(t)
  • allgemeine Lösung dann
    • x(t) = x_hom(t) + x_spez(t)
  • wenn Summe als Inhomogenität
    • f = f₁ + f₂
    • x_i Lösung zu f_i (i = 1,2)
    • ⇒ x = x₁ + x₂ ist Lösung zu f