Linearisierung von Bewegungsgleichungen
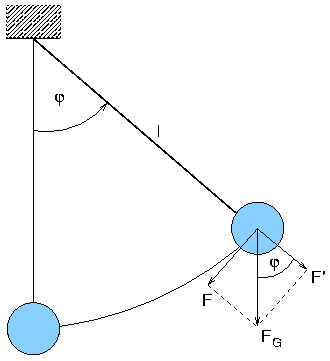
- Beispiel Fadenpendel:
- Masse an einem Faden unter Gewichtskraft
- Idealisierungen
- keine Reibungsverluste
- Faden gewichtslos und undehnbar
- Faden ist stabil bei großen Winkeln
("Stange")
- rücktreibende Kraft
- Bewegungsgleichung aus Momentengleichgewicht
- d2φ/dt2 + (g/l) sin
φ = 0
- Lösung der Bewegungsgleichung:
- nichtlinear → schwierig
- hier analytisch möglich, aber aufwändig
- numerische Lösung
- im Phasenraum
- neue Phänomene
- Abhängigkeit der Schwingungsdauer von der
Amplitude
- unbeschränkter Winkel (Überschlag)
- Näherung kleiner Schwingungen:
- Annahme kleiner Auslenkungen
- Gleichung näherungsweise linear
- in praktischen Anwendungen häufig gut erfüllt
- Vorgehensweise bei der Linearisierung:
- Bewegungsgleichung aufstellen
- stabile Gleichgewichtslage(n) bestimmen
- Koordinate x einführen mit x = 0 im
Gleichgewicht
- lineare Näherung für nichtlineare Kräfte durch
Taylorentwicklung
- komplett: f(x) = f(0) + x f'(0) + ...
- schrittweise: sin(x) ≈ x, exp(x) ≈
1 + x, x2 ≈ 0 etc.
- Einsetzen →
- lineare Gleichung
- Terme f(0) heben sich auf (Gleichgewicht)
- Linearisierung beim Fadenpendel:
- Gleichgewichtslagen
- Linearisierung um φ = 0
- x = φ
- sin x = x - 1/3! x3 + 1/5!
x5
 ...
...
- ⇒
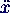 + (g/l) x = 0
+ (g/l) x = 0
- harmonische Schwingung mit
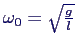
- Linearisierung um φ = π
- x = φ - π
- sin φ = sin(π + x) = - sin x
- ⇒
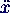 - (g/l) x = 0
- (g/l) x = 0
- x wächst exponentiell
- instabiles Gleichgewicht
- Aufgaben:



 ...
...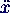 + (g/l) x = 0
+ (g/l) x = 0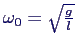
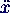 - (g/l) x = 0
- (g/l) x = 0