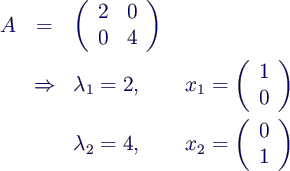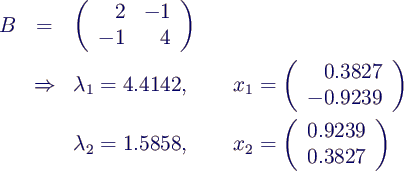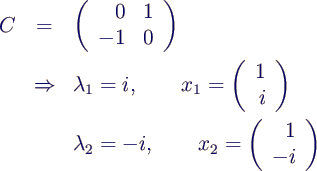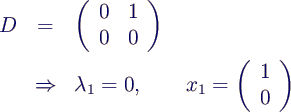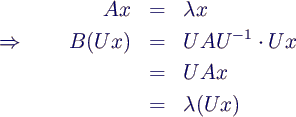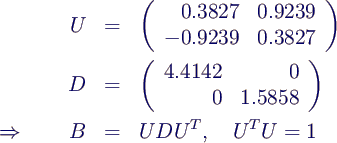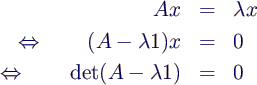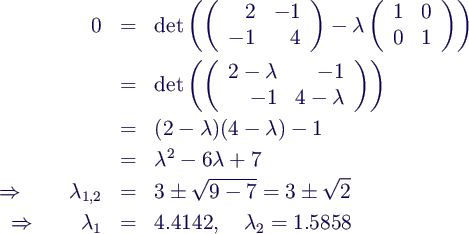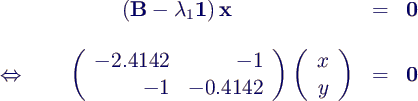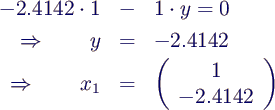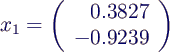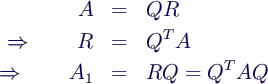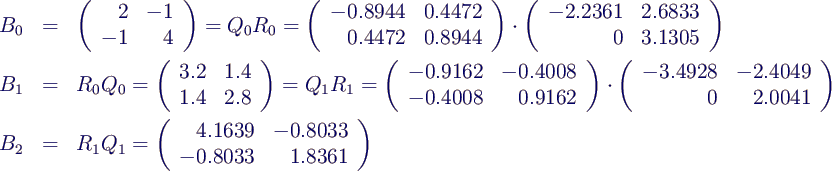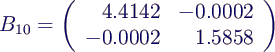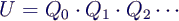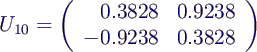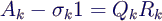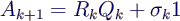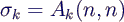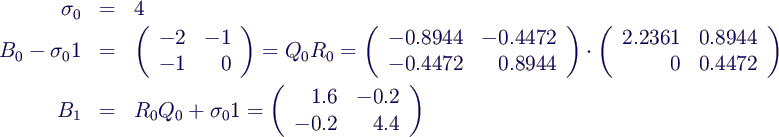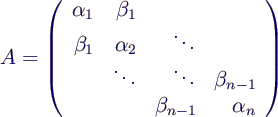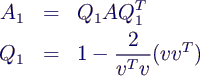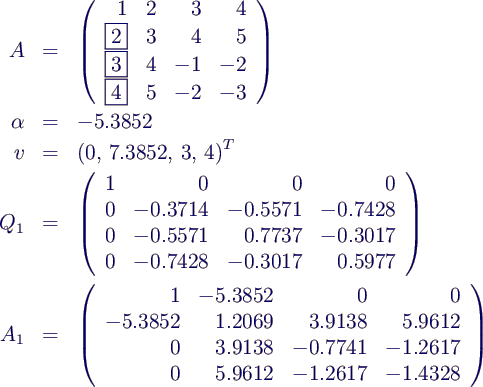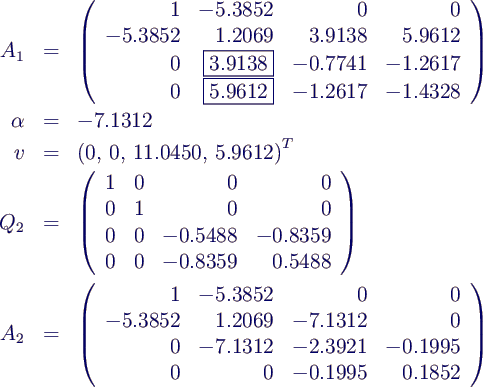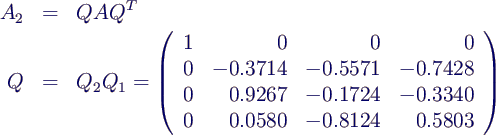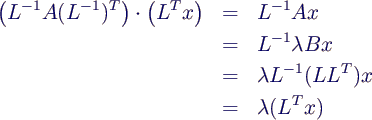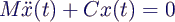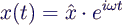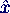Bestimmung von Eigenwerten und Eigenvektoren

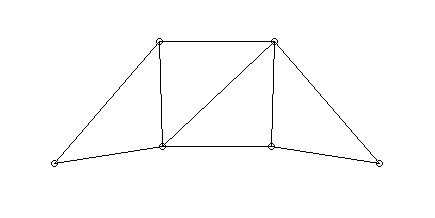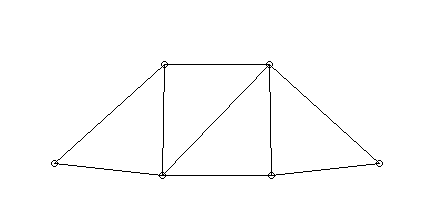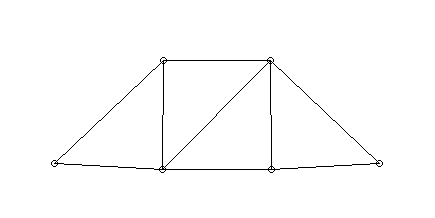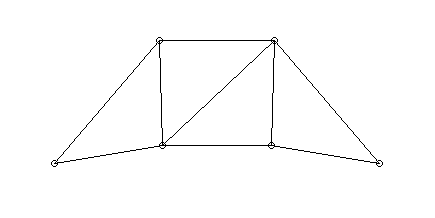
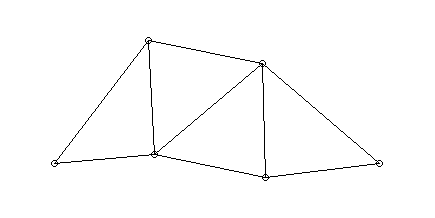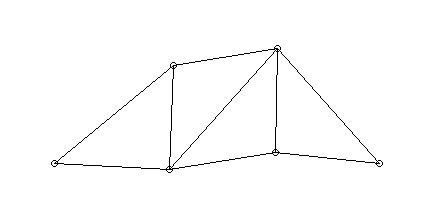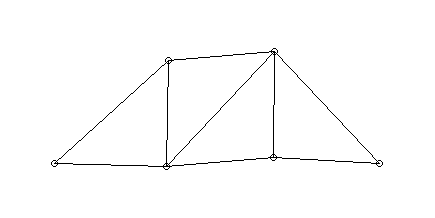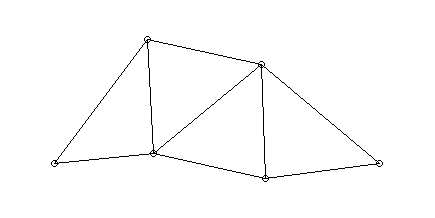
• Schwingungen eines Fachwerks:
  • Fachwerk
    • 
    • in den Punkten 5 und 6 fest gelagert
    • alle Knoten haben Masse m
    • Balken als Zug-/Druckfedern mit gleicher Federkonstante c
  • äußere Vibrationen wirken auf das Fachwerk (durch die Lager 5, 6)
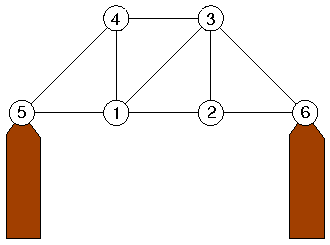
    • bei einigen Frequenzen heftiges Mitschwingen (Eigenfrequenzen)
    • jeweils typische Schwingungsformen (Eigenschwingungen)
    • 
• Definition der Eigenwertaufgabe:
  • gegeben sei eine nxn-Matrix A
  • gesucht sind Zahl λ und Vektor x ≠ 0 mit
    • A x = λ x
  • λ heißt Eigenwert von A, x Eigenvektor von A zum Eigenwert λ
  • Länge von x beliebig, häufig auf 1 gesetzt (oder größte Komponente auf 1)
  • Beispiel 1 (Diagonalmatrix)
    • 
  • Beispiel 2 (symmetrische Matrix)
    • 
  • Beispiel 3 (unsymmetrische Matrix)
    • 
  • Beispiel 4 (nur 1 Eigenvektor)
    • 
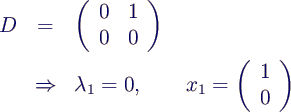
    • kein weiterer Eigenwert und Eigenvektor (bis auf Faktor)
• Eigenschaften von Matrizen:
  • besondere Matrizen
    • A^T = A (symmetrisch)
    • A^T A = 1 (orthogonal, z.B. Drehungen und Spiegelungen)
    • (x, Ax) ≥ 0 für bel. Vektor x (positiv)
  • Ähnlichkeitstransformation
    • B = U A U^-1  (U beliebig, aber invertierbar)
  • Satz:
    • Ähnliche Matrizen A und B haben gleiche Eigenwerte
    • x Eigenvektor von A ⇒ Ux Eigenvektor von B
    • Beweis
    • 
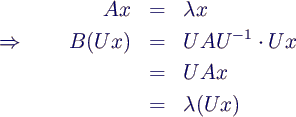
  • Satz:
    • Sei A symmetrisch. Dann ist A zu einer reellen Diagonalmatrix D ähnlich, wobei die Transformationsmatrix U orthogonal ist:
    • A = U D U^T mit U^T U = 1
    • Insbesondere sind alle Eigenwerte reell, der k-te Eigenvektor ist die k-te Spalte von U.
    • Beweis: z.B. in [8]
  • etwa bei Beispiel 2
    • 
  • betrachten i.F. nur symmetrische Matrizen
• Analytische Berechnung von Eigenwerten und -vektoren:
  • A nxn-Matrix, dann gilt für ein x ≠ 0
    • 
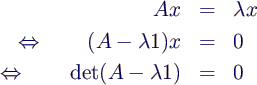
    • also Polynom der Ordnung n für λ (charakteristisches Polynom von A)
    • hat n Lösungen (davon können mehrere zusammenfallen)
  • für Beispiel 2
    • 
  • Eigenvektor x₁ als Lösung des homogenen System
    • 
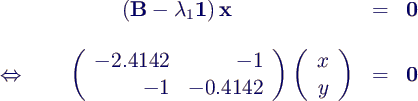
    • 1. Komponente willkührlich auf 1 setzen →
    • 
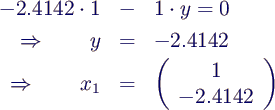
    • Vektor normieren (Länge 1) durch Multiplikation mit 0.3827 →
    • 
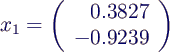
    • analog für x₂
  • Verfahren für größeres n wenig brauchbar
    • keine Lösungsformeln für n > 4
    • Nullstellensuche von Polynomen i.a. schlecht konditioniert
• QR-Verfahren:
  • Grundidee:
    • Transformiere A mit geschickt gewähltem orthogonalen U
    • A' = U^T A U
    • so dass A' größere Diagonal- und kleinere Nichtdiagonalelemente hat als A
    • Wiederhole, bis A' nahezu diagonal
  • Prinzip des QR-Verfahrens
    • Mache QR-Zerlegung von A
    • A₀ = Q R
    • neues A ist A₁ = R Q
    • dies ist eine Ähnlichkeitstransformation, denn
    • 
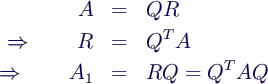
  • im Beispiel
    • 
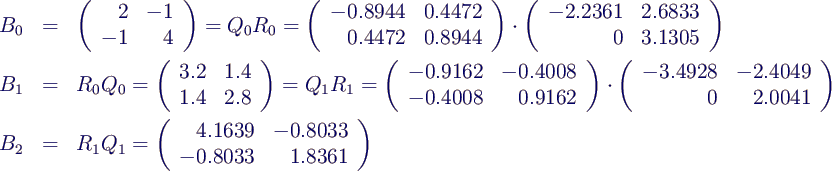
    • nach 10 Iterationen wird aus B
    • 
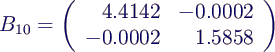
    • U (und somit die Eigenvektoren) erhält man aus
    • 
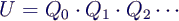
    • nach 10 Iterationen
    • 
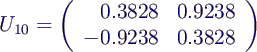
  • Konvergenz-Beschleunigung durch Shift
    • verschiebe Eigenwerte vor der QR-Zerlegung um σ_k
    • 
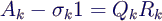
    • schiebe hinterher wieder zurück
    • 
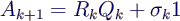
    • sinnvoller Wert für σ_k: rechte untere Ecke von A_k
    • 
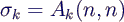
  • im Beispiel
    • 
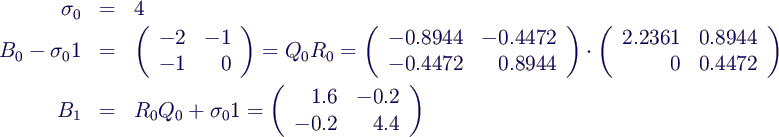
    • schon nach 3 Iterationen erhält man die Ergebnismatrizen auf 4 signifikante Stellen
• Symmetrische Hessenberg-Form:
  • QR-Verfahren konvergiert erheblich schneller für Tridiagonalmatrizen (symmetrische Hessenberg-Matrizen)
    • 
  • kann durch Transformation mit n-2 Householdermatrizen (s. QR-Zerlegung) aus beliebiger symmetrischer Matrix erreicht werden
    • 
  • 1. Schritt mit folgendem Vektor v
    • 
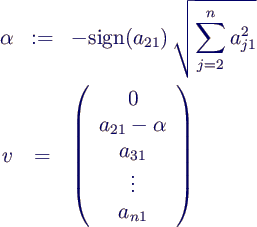
    • folgende Schritte mit Teilmatrizen
  • Beispiel
    • 1. Schritt
    • 
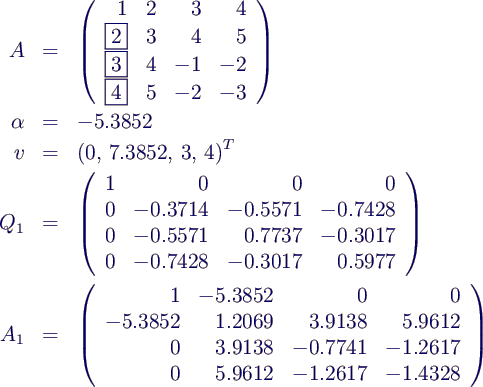
    • 2. Schritt
    • 
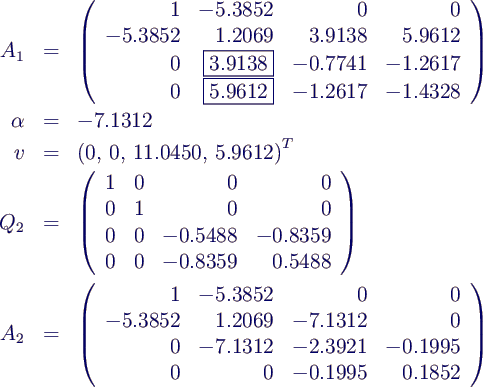
    • zusammen
    • 
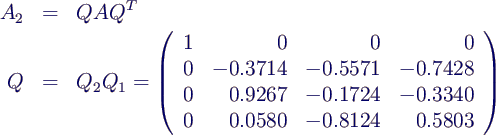
• Verallgemeinertes Eigenwert-Problem (VEP):
  • gegeben seien zwei nxn-Matrix A, B
  • gesucht sind Zahl λ und Vektor x ≠ 0 mit
    • A x = λ B x
  • wichtiger Spezialfall: A, B symmetrisch, B positiv und nicht singulär
  • dann auf normales Eigenwert-Problem zurückführbar
    • Cholesky-Zerlegung von B
    • B = L L^T
    • dann gilt
    • 
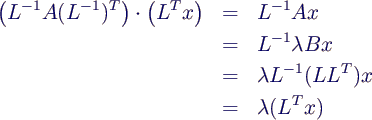
  • also:
    • Eigenwert λ und Eigenvektor x von L^-1 A (L^-1)^T bestimmen
    • λ ist Eigenwert des VEP
    • (L^-1)^T x ist Eigenvektor des VEP
• Matlab-Funktionen:
  • Lösung des Eigenwertproblems
    • [U,D] = eig(A)
    • A = U D U^T, U^T U = 1, D diagonal
    • Eigenwerte = Werte aus diag(D)
    • Eigenvektoren = Spalten von U
  • Lösung des verallgemeinerten Eigenwertproblems
    • [U,D] = eig(A,B)
    • Bedeutung wie bei eig
  • Hessenberg-Matrix zu A
    • [Q,H] = hess(A)
    • A = Q H Q^T mit Q^T Q = 1
• Anwendung auf Schwingungsprobleme:
  • Bewegungsgleichung für kleine Schwingungen (frei und ungedämpft)
    • 
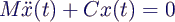
    • x(t): Vektor der Koordinaten, Auslenkungen aus der Gleichgewichtslage
    • M: symmetrische, positive Matrix (Massenmatrix)
    • C: symmetrische, positive Matrix (Steifigkeitsmatrix)
  • Ansatz
    • 
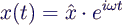
    • liefert
    • 
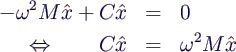
  • also verallgemeinertes Eigenwert-Problem mit
    • Eigenwert ω²
    • Eigenvektor
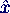
  • Lösung liefert Schwingung mit Eigenfrequenz ω = 2 π f
• Aufgaben:
  • Aufgabe 15
  • Aufgabe 16