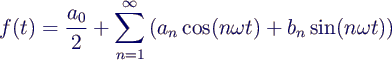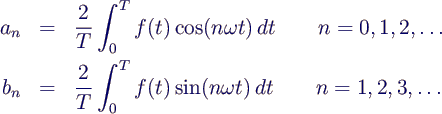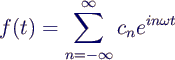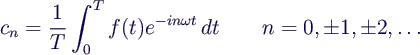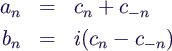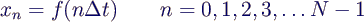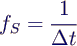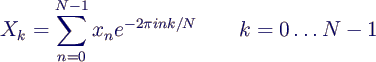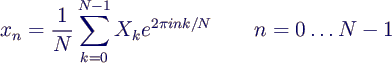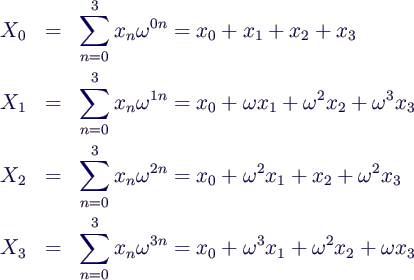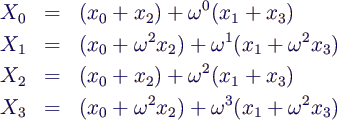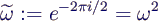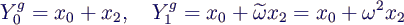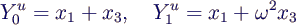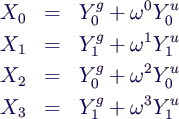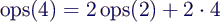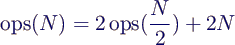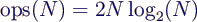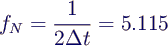Fourieranalyse

• Analyse von Störschwingungen:
  • seltsame Störungen in einer Maschine, hervorgerufen durch Vibrationen unbekannter Herkunft
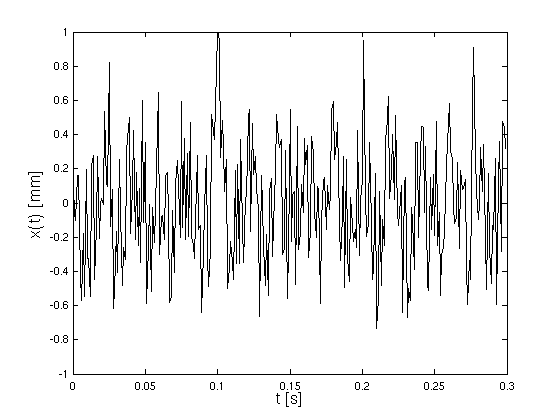
  • Messung der Vibrationen ergibt
    • 
  • Spektralanalysator zeigt
    • 
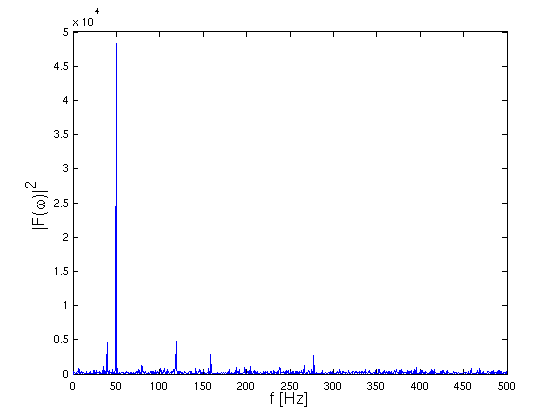
    • große Spitze bei 50 Hz
    • Spitzen in festen Frequenzabständen (Grundfrequenz 39.6 Hz)
    • Untergrund bei allen Frequenzen
  • Interpretation
    • Rauschen (Messfehler + allgemeine Störungen) als Untergrund
    • Trafoschwingungen bei 50 Hz
    • besondere Störung mit Grundfrequenz 39.6 Hz
• Fourierreihe:
  • Zerlegung einer periodischen Funktion f(t) mit Schwingungsdauer T in Sinus- und Kosinus-Schwingungen
    • 
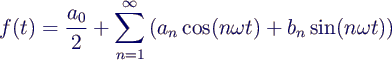
    • mit ω := 2 π/T
  • Berechnung der Koeffizienten
    • 
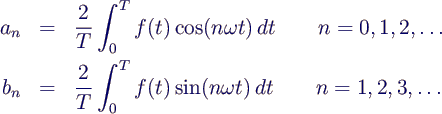
    • liefert bei endlicher Reihe beste Approximation "im quadratischen Mittel" [11]
    • konvergiert für stückweise stetiges beschränktes f im Mittel [11]
  • Zusammenfassung als komplexe e-Funktion
    • 
  • Berechnung der komplexen Koeffizienten
    • 
  • Bestimmung von a_n und b_n aus c_n
    • 
• Beispiel Sägezahnschwingung:
  • f(t) = t/2 für t = -π .. π
    • 
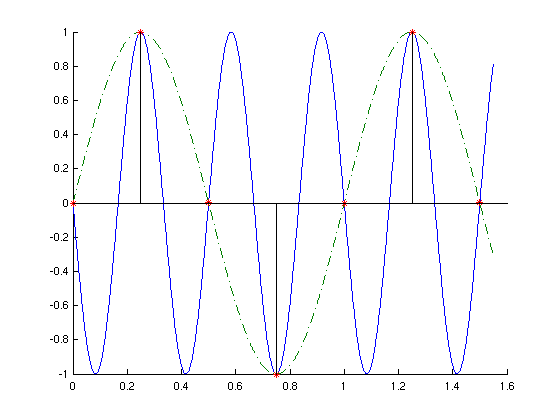
  • Aufbau aus Grund- und Oberschwingungen
    • 
  • als Applet zum Experimentieren
    • 
  • Koeffizienten
    • 
  • Fourierreihe also
    • f(t) = sin(t) - 1/2 sin(2t) + 1/3 sin(3t) - 1/4 sin(4t) ...
  • Spektrum (Darstellung der Größe der Koeffizienten über der Frequenz)
    • 
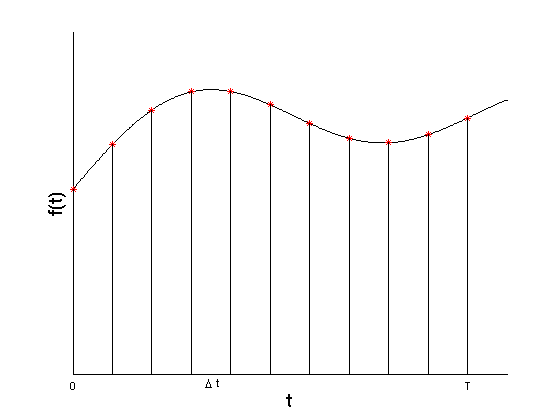
• Abtasten einer Funktion (Sampling):
  • in der Praxis Funktion f meistens nicht explizit bekannt
  • stattdessen werden Werte der Funktion f in festen Zeitabständen Δt gemessen
    • 
    • 
  • z.B. Messung im Schwingstand alle 1/100 s
  • Abtastfrequenz (Sampling rate)
    • 
  • insgesamt N Werte, also Messdauer
    • T = (N-1) Δt
• Diskrete Fouriertransformation:
  • Ausgangspunkt sind N Werte x_n, n = 0, .. N - 1 (gemessen in festen Zeitabständen Δt)
  • Berechnung der diskreten Fouriertransformierten X(k) (analog zu c_k) mit
    • 
  • Rücktransformation
    • 
  • Achtung:
    • nur Schwingungen bis zur Nyquist-Frequenz f_N = f_S/2 messbar
    • Schwingungen höherer Frequenz f tauchen bei niedrigeren Werten 2 f_N - f auf (Aliasing)
    • 
• Fast Fourier Transformation (FFT):
  • Zahl der Operationen ops(N) (Multiplikationen + Additionen) bei direkter Berechnung von X_k
    • N Multiplikationen, N-1 Additionen für ein X_k
    • N² Multiplikationen, N*(N-1) Additionen für alle X_k
    • → ops(N) = 2*N² - N
  • starke Reduktion des Aufwands bei geradem N mit "Umsortier-Trick"
  • Beispiel N = 4
    • Mit der Abkürzung
    • 
    • erhält man die Fouriertransformierte X_n
    • 
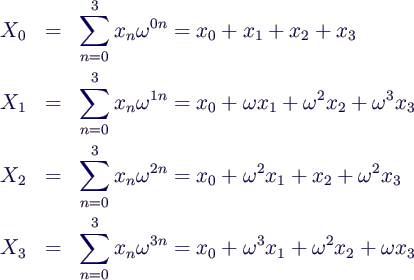
    • was sich umsortieren lässt zu
    • 
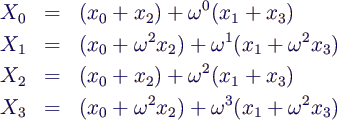
    • Die Fouriertransformierte Y^g_n der "geraden Werte" x₀ und x₂ berechnet man mit
    • 
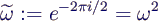
    • zu
    • 
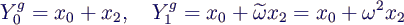
    • Analog ist die Fouriertransformierte Y^u_n der "ungeraden Werte" x₁ und x₃
    • 
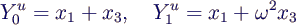
    • Also kann man die Fouriertransformierte der 4 Werte auf die von jeweils 2 zurückführen
    • 
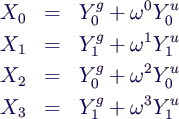
    • Für die Zahl der Operationen ergibt sich somit
    • 
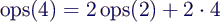
  • ganz analog zeigt man für beliebiges gerade N (s. Anhang)
    • 
  • falls N eine Zweierpotenz ist, folgt aus dieser Beziehung durch wiederholte Anwendung des "Umsortier-Tricks" (s. Anhang)
    • 
  • dies ist für große N eine dramatische Zeitersparnis, etwa bei 1 ns pro Operation

    • N	ops normal	ops FFT
      1024	2 ms	20 μs
      1048576	2199 s	0.042 s
      1073741824	73 a	64 s

    • 1000x1000 Fouriertranformationen häufig (z.B. Bildbearbeitung)
  • man wählt (fast) immer N als Zweierpotenz, notfalls mit Nullen auffüllen
• FFT mit Matlab:
  • grundlegende Funktionen
    • X = fft(x);
    • x = ifft(X);
  • da X komplex, häufig nur Betrag oder Betragsquadrat (Leistungsspektrum) interessant
    • F = abs(X)
  • Darstellung des Spektrums
    • nur bis zur zulässigen Maximalfrequenz
    • x-Achse in richtigen Einheiten (z.B. in Hz)
    • Matlabvektoren beginnen bei 1, Frequenzen fangen bei 0 an
    • → Indizes um 1 verschieben
• Anwendungsbeispiel in Matlab:
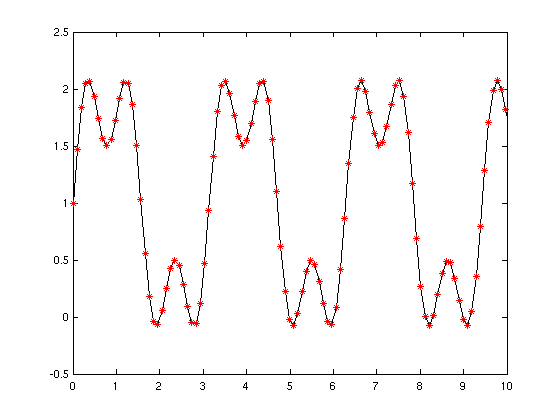
  • Ausgangsfunktion
    • f = @(t) 2 + sin(2*t) + 0.5*sin(6*t);
  • gesampelt über Zeit T, N Werte
    • T = 100;
      N = 1024;
      Delta_t = T/(N-1);
      t = [0:N-1]*Delta_t;
      x = f(t);
  • Samplewerte (Ausschnitt!)
    • 
  • FFT
    • X = fft(x);
      F = abs(X(1:N/2))/N;
      freq = [0:(N/2)-1]/T;
      plot(freq, F);
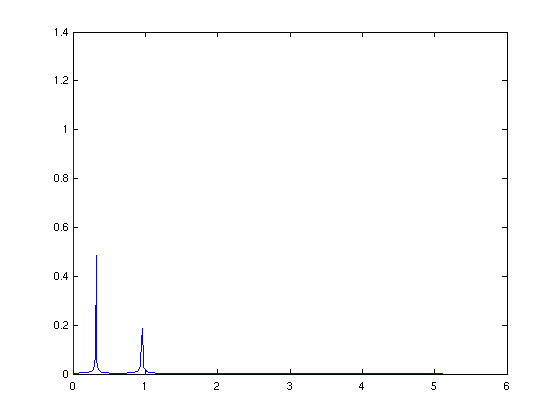
  • Spektrum
    • 
  • maximale Frequenz (Nyquist-Frequenz)
    • 
  • Wert bei f = 0 ist Mittelwert
• Aufgaben:
  • Aufgabe 13
  • Aufgabe 14