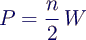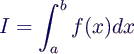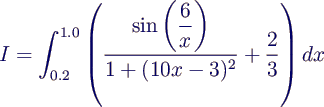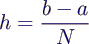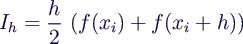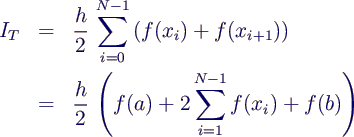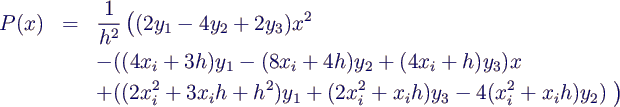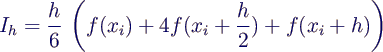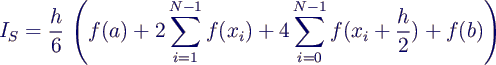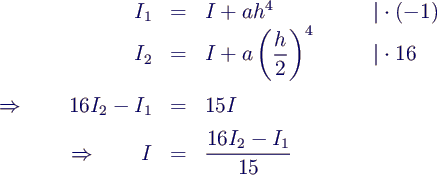Numerische Integration

• Leistung eines Otto-Motors:
  • vereinfachter Kreisprozess
    • 1 → 2 Kompression ohne Wärmezufuhr (adiabatisch)
    • 2 → 3 Zündung → sehr schnelle Drucksteigerung, Wärmezufuhr näherungsweise bei konstantem Volumen
    • 3 → 4 adiabatische Ausdehnung
    • 4 → 1 Druckminderung bei konstantem Volumen, Ausstoßen der Abgase, Ansaugen des neuen Gemischs
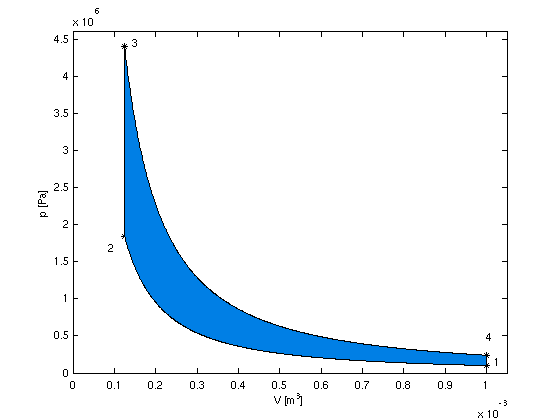
  • Darstellung von Druck über Volumen (p-V-Diagramm)
    • 
  • umschlossene Fläche = abgegebene Arbeit W bei einem Umlauf
  • Leistung P bei Motordrehzahl n
    • 
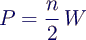
    • (Arbeitstakt nur jede 2. Umdrehung)
  • realistischer mit Modell für Verbrennungsvorgang
    • 
• Problemstellung:
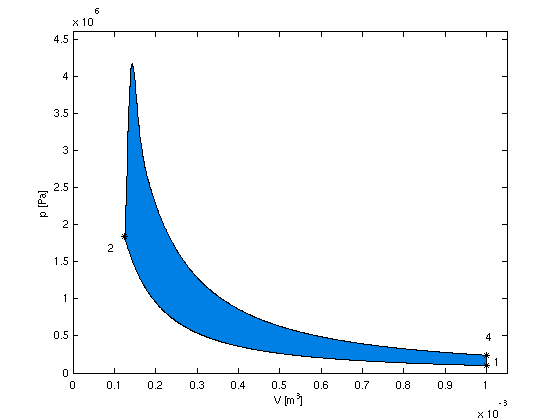
  • berechne für gegebene Funktion f und gegebene Grenzen a, b das bestimmte Integral
    • 
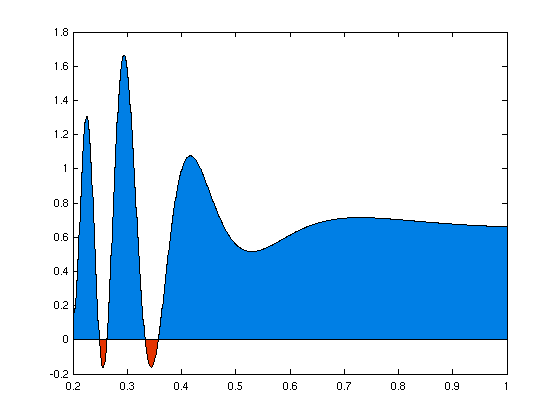
  • Standardbeispiel im Folgenden
    • 
  • im Bild
    • 
  • Wert
    • I = 0.535914332007100
• Trapezregel:
  • Aufteilen des Intervalls [a, b] in N Teilintervalle [x_i, x_i+1] (x₀ = a, x_N = b) der Länge
    • 
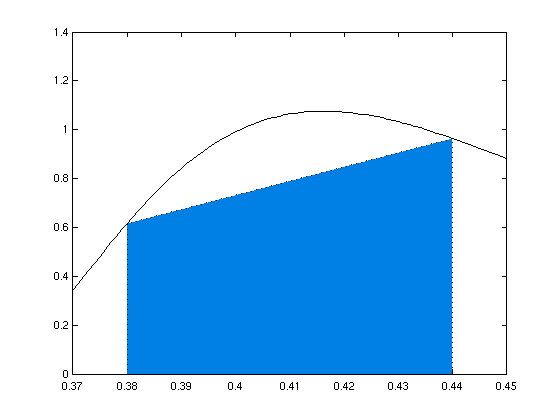
  • Approximation von f auf einem Teilintervall [x_i, x_i + h] durch eine Gerade durch die Randpunkte (x_i, f(x_i)) und (x_i+1, f(x_i+1))
    • 
  • Integralnäherung auf dem Intervall
    • 
  • Näherung des gesamten Integrals durch Addition
    • 
  • Genauigkeit O(h²) [8]
  • im Standardbeispiel

    • h	IT	rel. Fehler
      1.000000e-01	0.62504156147227	1.663087e-01
      1.000000e-02	0.53605438650191	2.613375e-04
      1.000000e-03	0.53591569981964	2.552297e-06
      1.000000e-04	0.53591434568167	2.551634e-08
      1.000000e-05	0.53591433214385	2.551738e-10
      1.000000e-06	0.53591433200846	2.539420e-12
      1.000000e-07	0.53591433200717	1.282347e-13

  • Verfahren leicht auf unterschiedliche Intervallgrößen erweiterbar
    → gut geeignet für durch Messwerte gegebene Funktionen
• Simpsonregel:
  • Idee wie bei Trapezregel, aber f durch Parabel approximieren
    • 
  • Parabel durch Punkte bei x_i, x_i + h/2, x_i + h
    • 
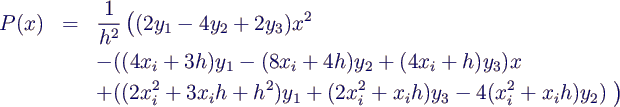
    • mit y₁ = f(x_i), y₂ = f(x_i + h/2), y₃ = f(x_i + h)
  • Integralnäherung auf dem Intervall
    • 
  • Näherung des gesamten Integrals durch Addition
    • 
  • Genauigkeit O(h⁴) (!) [8]
  • im Standardbeispiel

    • h	IS	rel. Fehler
      1.000000e-01	0.47345537553892	1.165465e-01
      1.000000e-02	0.53591352330050	1.509022e-06
      1.000000e-03	0.53591433191739	1.673978e-10
      1.000000e-04	0.53591433200709	1.553732e-14
      1.000000e-05	0.53591433200710	2.693136e-15
      1.000000e-06	0.53591433200709	1.553732e-14

• Verbesserung der Verfahren:
  • höhere Polynom-Ordnung bringt nichts, da höhere Interpolationspolynome stark schwingen
  • zwei versch. Ansätze
    • Erhöhung der Ordnung durch Extrapolation
    • feste Ordnung, aber Anpassung der Schrittweite
• Adaptives Simpson-Verfahren:
  • Grundidee: Intervalle dort verfeinern, wo Teilergebnis ungenauer als vorgegebene Toleranz δ
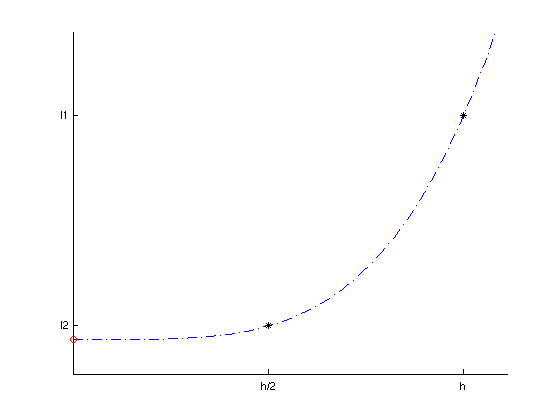
  • Fehler-Abschätzung auf einem Teilintervall der Breite h
    • ein Simpson-Schritt → I₁
    • Intervall halbieren, zwei Simpson-Schritte → I₂
    • | I₂ - I₁ | < δ → Schritt ok
    • sonst: Intervall halbieren und mit jedem Teilintervall weitermachen
  • Ergebnis I₂ kann noch verbessert werden durch Extrapolation
    • 
    • 
  • extrapolierter Wert hat höhere Fehlerordnung (hier O(h⁶)!)
  • Gesamtfehler a priori schwer abschätzbar
    • Einzelfehler können viel kleiner sein als δ
    • Anzahl der Intervalle variabel
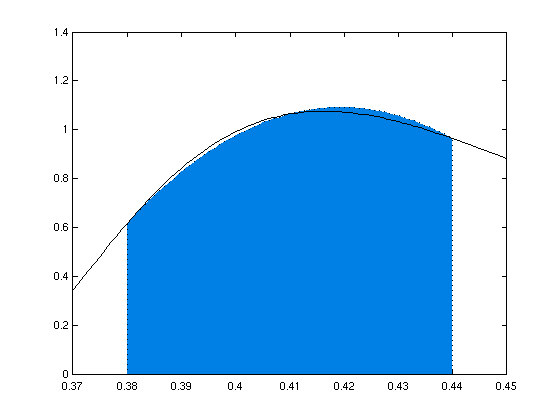
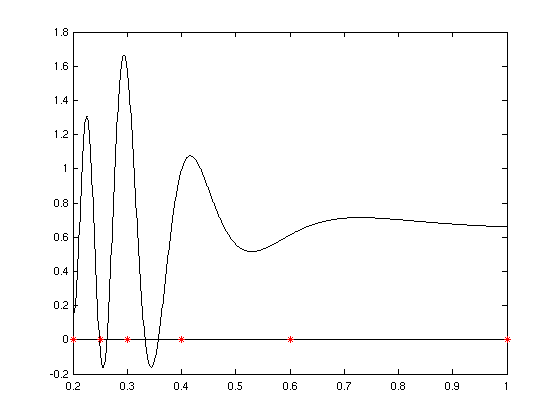
• Adaptive Integration am Beispiel:
  • Standardbeispiel mit Genauigkeit δ = 0.02
    1. l = 0.200, r = 1.000 → I1 = 0.4377, I2 = 0.5891 halbieren
    2. l = 0.200, r = 0.600 → I1 = 0.3168, I2 = 0.3775 halbieren
    3. l = 0.600, r = 1.000 → I1 = 0.2723, I2 = 0.2743 ok
    4. l = 0.200, r = 0.400 → I1 = 0.2494, I2 = 0.0598 halbieren
    5. l = 0.400, r = 0.600 → I1 = 0.1280, I2 = 0.1393 ok
    6. l = 0.200, r = 0.300 → I1 = 0.0254, I2 = 0.0848 halbieren
    7. l = 0.300, r = 0.400 → I1 = 0.0345, I2 = 0.0458 ok
    8. l = 0.200, r = 0.250 → I1 = 0.0445, I2 = 0.0355 ok
    9. l = 0.250, r = 0.300 → I1 = 0.0403, I2 = 0.0391 ok
  • Ergebnis: I = 0.5350 (exakt: 0.5359)
  • Verteilung der Intervalle
    • 
• Probleme bei der Integration:
  • Pseudo-Singularitäten (sin(x)/x)
  • Singularitäten am Rand
  • Singularitäten im Intervall → Integral aufspalten
  • unendliche Intervalle
• Matlab-Funktionen:
  • Integration mit adaptivem Verfahren
    • I = integral(fun, a, b)
  • mit Vorgabe der Genauigkeit
    • I = integral(fun, a, b, "RelTol", tol)
  • alternatives Verfahren, auch bei Singularitäten am Rand oder unendlichem Intervall
    • I = quadgk(fun, a, b) mit Standardgenauigkeit
    • I = quadgk(fun, a, b, "AbsTol", tol) mit absoluter Genauigkeit tol
    • I = quadgk(fun, a, b, "RelTol", tol) mit relativer Genauigkeit tol
  • Berechnung des Integrals zu Messpunkten X, Y mit Trapezregel
    • I = trapz(X,Y)
• Weitere Methoden:
  • sukzessive Erhöhung der Ordnung durch Extrapolation (Romberg-Verfahren)
  • Wahl von Stützpunkten mit verschiedenem Abstand (Gauß-Formeln)
  • Integral als Lösung der Differentialgleichung
    • y' = f(x), y(0) = a
    • Lösung bis y(b)
  • Mehrfach-Integrale
    • i.a. schwierig
    • komplizierte Integrationsgebiete statt einfachem Intervall
    • viele ganz spezifische Verfahren (z. B. Montecarlo-Integration)
• Aufgaben:
  • Aufgabe 17
  • Aufgabe 18