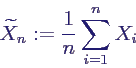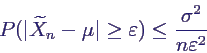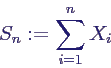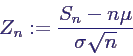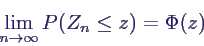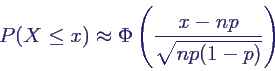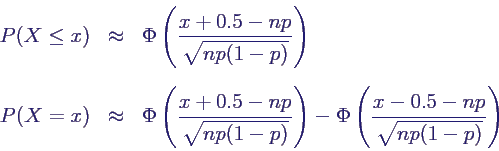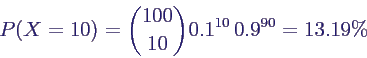Grenzwertsätze
- Tschebyschoff-Ungleichung:
- X Zufallsvariable mit E(X) = μ, Var(X) = σ2,
c > 0 beliebig ⇒
- anschaulich: Abweichung einer Zufallsgröße
vom Mittelwert selten größer als einige σ
- Beweis der Tschebyschoff-Ungleichung:
- Betrachte diskrete Zufallsgröße Y gegeben
durch
- Offensichtlich gilt
- Daher ist Erwartungswert
- Außerdem ist
- Daraus folgt
- (Schwaches) Gesetz der großen Zahlen:
- Xi Folge von i.i.d. Zufallsvariablen
mit E(Xi) = μ, Var(Xi) = σ2,
ε > 0 beliebig ⇒
- anschaulich: Mittelwert geht mit Wahrscheinlichkeit 1
gegen Erwartungswert
- Stärkere Version (Mittelwert geht gegen
Erwartungswert) ist falsch, da dauerhafte große Abweichungen
möglich sind (wenn auch unwahrscheinlich).
- Spezialfall
- Xi ~ B(1,p), d.h. Eintreffen eines
Ereignisses A mit Wahrscheinlichkeit p
- E(Xi) = p
- Mittelwert der Xi = relative
Häufigkeit des Eintretens von A
- Satz sagt: Relative Häufigkeit geht nach
Wahrscheinlichkeit gegen p
- nachträgliche Begründung für
Frequentismus (s.o.)
- Beweis des Gesetzes der großen Zahlen:
- Definiere Zufallsgröße
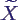 n
n
- Wegen Unabhängigkeit der Xi addieren
sich Erwartungswerte und Varianzen. Daher
- Einsetzen in Tschebyschoff-Ungleichung ⇒
- mit n → ∞ folgt Behauptung
- Zentraler Grenzwertsatz:
- Xi Folge von i.i.d. Zufallsvariablen mit
E(Xi) = μ, Var(Xi) = σ2
- betrachte Summenverteilung
- Fakt: Sn geht gegen Normalverteilung, aber
- E(Sn) = n μ, Var(Sn) = n
σ2
- gehen im Limes gegen unendlich, daher
mathematisch unbequem
- Ausweg: standardisierte Verteilung betrachten
- Satz: Verteilung von Zn geht gegen
Standardnormalverteilung
- Beweis aufwändig
- Satz verallgemeinerbar auf nicht-identische
Verteilungen (unter bestimmten Voraussetzungen)
- Grund für häufiges Auftreten der
Normalverteilung, z.B.
- Messfehler oder Produktionsungenauigkeiten oft
Summe vieler kleiner Einzelfehler
- Größe von Menschen durch viele
verschiedene Parameter bestimmt
- Approximation der Binomialverteilung:
- Einzelverteilung Xi = B(1,p), i = 1, .. n
- Eintreffen eines Ereignisses A mit
Wahrscheinlichkeit p
- X = Σ Xi = Anzahl der Treffer ~ B(n,
p)
- Binomialverteilung nähern durch Normalverteilung
- Stetigkeitskorrektur
- Treppenfunktion → glatte Dichtefunktion
- genauer, wenn Dichtefunktion Stufen in der Mitte
trifft
- besser also
- Anwendungsbereich
- n p und n (1-p) groß genug
- Faustregel: beide ≥ 5
- Beispiel Produktionsfehler (s.o.):
- Fehlerquote p = 10 %, entnommen werden n = 100
Stück
- Check: n p = 10, n (1-p) = 90 → Näherung ok
- Berechnung von P(X = 10) mit Binomialverteilung
- Berechnung von P(X = 10) mit Normalverteilung
- Aufgaben:



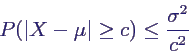
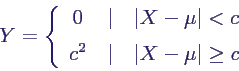
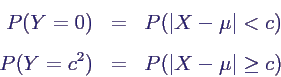
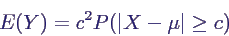
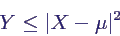
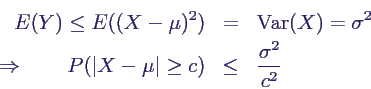
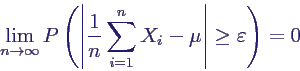
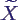 n
n