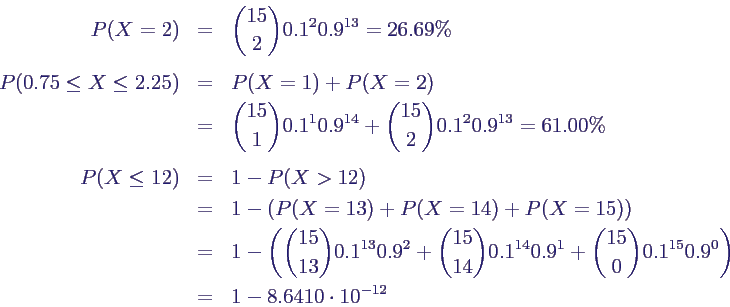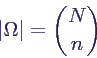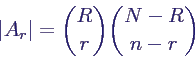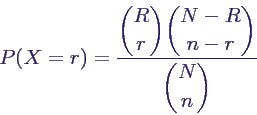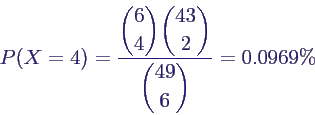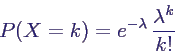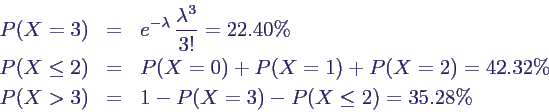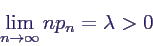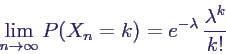Spezielle diskrete Verteilungen
- Gleichverteilung:
- mögliche Werte 1, ..., N
- p(k) = 1/N für k = 1, ..., N
- Beispiele: Münzwurf, Würfeln
- Binomialverteilung B(n,p):
- Bernoulli-Experiment
- Experiment mit zwei Ausgängen ("Erfolg",
"Misserfolg")
- Wahrscheinlichkeit für Erfolg sei p
- X = Anzahl von Erfolgen bei n-maliger Wiederholung
- Wahrscheinlichkeitsfunktion
- Begründung
- ein bestimmtes Ereignis mit k Erfolgen hat
Wahrscheinlichkeit pk (1-p)n-k
- es gibt
 viele solcher Ereignisse
viele solcher Ereignisse
- Schreibweise
- X ~ B(n,p) :⇔ X ist verteilt nach B(n,p)
- analog für andere Verteilungen
- Anwendung Produktionsfehler:
- Bei einer Stanzmaschine seien 10% der gefertigten
Teile außerhalb der benötigten Toleranz und müssen
nachgearbeitet werden.
- Stichprobe mit 15 Teilen werde entnommen, X = Zahl
der defekten Bauteile
- Wahrscheinlichkeiten gesucht für
- genau zwei defekte Teile
- Zahl der defekten Teile zwischen 5% und 15%
- höchstens 12 defekte Teile
- Lösungen
- Geometrische Verteilung G(p):
- X = Zahl der Versuche, bis Bernoulli Erfolg liefert
- Wahrscheinlichkeitsfunktion
- p(k) = (1 - p)k-1 p für k = 1,
2, ...
- Beispiel Produktionsfehler
- Wie groß ist die Wahrscheinlichkeit, dass
erst das 5. Teil defekt ist?
- p(X = 5) = (1 - p)4 · p =
6.56%
- manchmal zählt man nur Zahl der Fehlversuche Y
- p(Y = k) = (1 - p)k p für k = 0,
1, ...
- Verteilung von Y heißt auch G0(p)
- Hypergeometrische Verteilung H(N, R, n):
- Grundmodell
- Urne enthalte N Kugeln, R rote, N-R weiße
- man zieht n Kugeln ohne Zurücklegen
- X = Anzahl der gezogenen roten Kugeln
- Zahl der möglichen Ziehungen insgesamt
- Zahl der Ziehungen mit genau r roten Kugeln
- Wahrscheinlichkeitsverteilung von X
- Beispiel Lottozahlen:
- wie üblich werden 6 aus 49 gezogen
- Vorstellung: die gezogenen werden rot bemalt
- X = Zahl der richtigen, hypergeometrisch verteilt
- insbesondere für 4 Richtige
- Poisson-Verteilung Po(λ):
- Verteilung für häufige Experimente mit
kleiner Erfolgs-Wahrscheinlichkeit
- X = Zahl der Erfolge in einem gegebenen Zeitintervall
- Beispiele
- Zahl von Schadensfällen pro Monat bei einer
Versicherung
- Zahl radioaktiver Zerfälle pro Sekunde
- Zahl der Fahrzeuge pro Minute auf einer
Straße
- Parameter λ = Rate, "mittlere" Zahl der
Erfolge pro Zeitintervall
- Wahrscheinlichkeitsverteilung von X
- Beispiel Versicherung:
- Annahme: Zahl der Schadensfälle ist
Poisson-verteilt mit Rate λ = 3/Monat
- berechne Wahrscheinlichkeiten folgender Ereignisse
- genau 3 Schadensfälle im Monat
- höchstens 2 Schadensfälle im Monat
- mehr als 3 Schadensfälle im Monat
- Lösungen
- Poisson-Grenzwertsatz:
- Betrachte binomialverteilte Zufallsvariablen Xn
mit Parametern n und pn, so dass
- Xn geht dann gegen eine Poissonverteilung,
d. h.
- Beweis im Anhang
- Aufgaben:



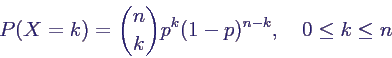
 viele solcher Ereignisse
viele solcher Ereignisse