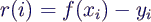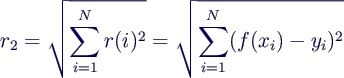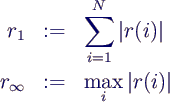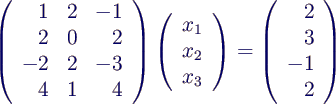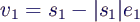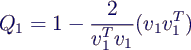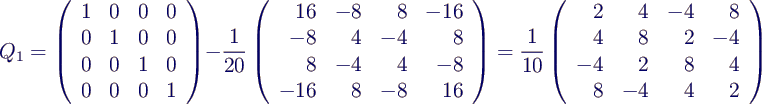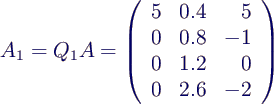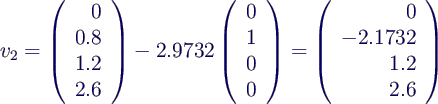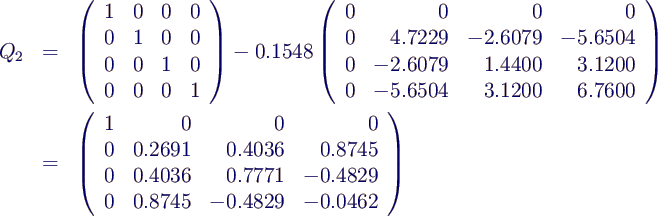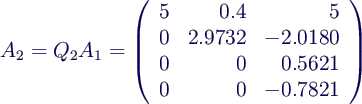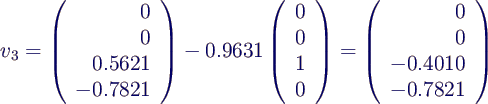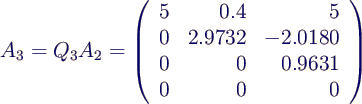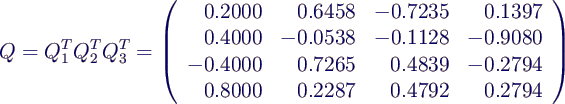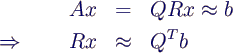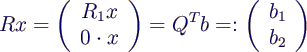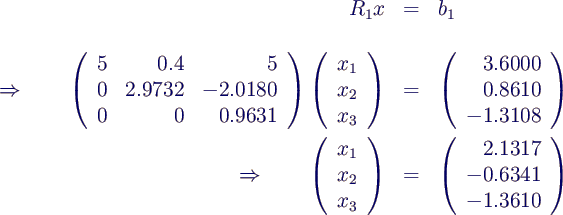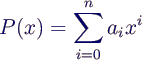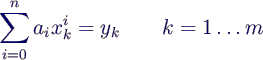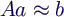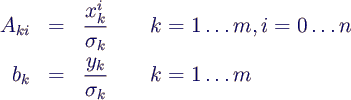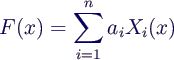Ausgleichsrechnung

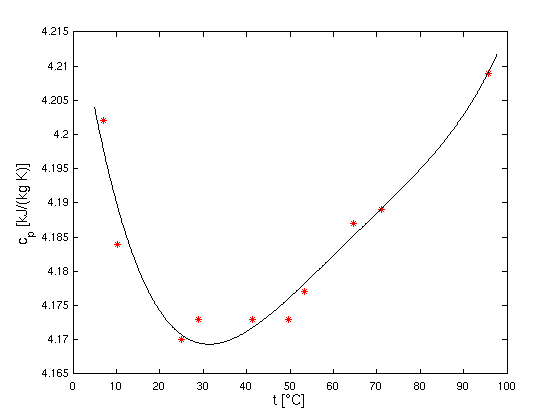
• Spezifische Wärmekapazität cp von Wasser:
  • Werte wie vorher
  • Idee:
    • Messwerte haben Fehler
    • Daten sollten durch Polynom 4. Ordnung gut beschrieben werden
  • gesucht: "bestes" Polynom zu den gegebenen Messwerten
    • 
• Problem der Approximation:
  • gegeben N Punkte (xi, yi), i = 1, .. N, mit xi ≠ xj für i ≠ j
  • gesucht Funktion f aus einer vorgegebenen Klasse (z. B. Polynom fester Ordnung), die "möglichst genau" durch die Punkte geht
  • Fehler von f bei Messung i
    • 
  • Gesamtfehler ("Methode der kleinsten Quadrate", "least square fit")
    • 
  • auch andere Gesamtfehler werden verwendet
    • 
  • Vorteil von r₂
    • führt auf numerisch gut zu lösende Gleichungen
    • liefert für normalverteilte Messwerte den "wahrscheinlichsten" Fit ("maximum likelihood")
• Lineare Ausgleichsrechnung:
  • lineares Gleichungssystem mit m Gleichungen für n Unbekannte (m > n)
    • A x = b
    • A mxn-Matrix, x n-Vektor, b m-Vektor
  • hat in der Regel keine Lösung
  • Beispiel
    • 
  • gesucht ist x mit minimalem quadratischen Fehler
  • kann berechnet werden als Lösung der Normalengleichung
    • (A^T A) x = A^T b
    • Beweis im Anhang
  • Lösung des nxn-Systems mit Gauß-Verfahren ist numerisch problematisch (schlecht konditioniert)
  • besser über QR-Zerlegung
    • Matrix A wird zerlegt in
    • A = Q R
    • mit
    • R = obere Dreiecksmatrix (unter der Diagonalen nur 0)
    • Q orthogonal (also Q^T Q = 1)
• QR-Zerlegung am Beispiel:
  • Prinzip
    • Durch Spiegelung an einer geeigneten Ebene (gegeben durch ihren Normalenvektor v) wird ein Spaltenvektor von A in Richtung eines Koordinatenvektors e_i gebracht
  • Basisvektoren: e₁, e₂, e₃
  • Spaltenvektoren der (transformierten) Systemmatrix: s₁, s₂, s_3,
  • 1. Schritt
    • berechne Hilfsvektor
      • 
      konkret
      • 
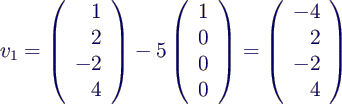
    • berechne Householdermatrix
      • 
      konkret
      • 
    • transformiere A
      • 
  • 2. Schritt:
    • berechne Hilfsvektor, ersetze dafür 1. Wert von s₂ durch Nullen →
      • 
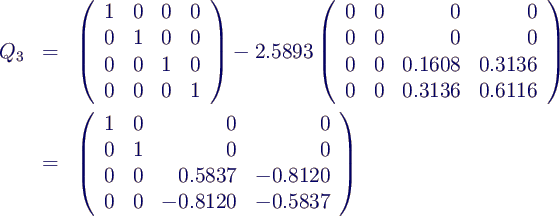
    • berechne Householdermatrix
      • 
    • transformiere A
      • 
  • 3. Schritt:
    • berechne Hilfsvektor, ersetze dafür 1. und 2. Wert von s₃ durch Nullen →
      • 
    • berechne Householdermatrix
      • 
    • transformiere A
      • 
  • damit ist eine obere Dreiecksmatrix erreicht, also
    • R = A₃
  • Da Q₁, Q₂ und Q₃ orthogonal sind (nachrechnen!), ist es auch
    • 
  • und es gilt
    • A = Q R
• Lösung der Normalengleichung:
  • Mit der QR-Zerlegung von A kann man schreiben
    • 
  • Da nur die oberen n Zeilen von R von 0 verschieden sind, teilt man das System in die oberen n und die unteren m-n Gleichungen
    • 
  • Die unteren Gleichungen kann man nicht lösen, sie liefern die Fehlerterme.
  • Die oberen Gleichungen liefern durch Rückwärtssubstitution die Lösung für x
  • Dieses x löst auch die Normalengleichung (Beweis im Anhang)
  • im Beispiel
    • Berechnung der rechten Seite
    • 
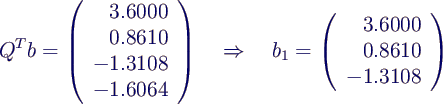
    • Lösen des Dreiecks-Systems
    • 
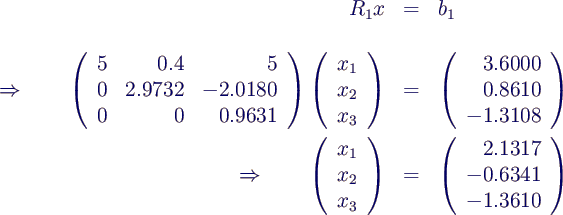
• Anwendung Polynomfit:
  • gegeben m Punkte (xi, yi), i = 1, .. m, mit xi ≠ xj für i ≠ j
  • gesucht: Polynom vom Grad n < m-1
    • 
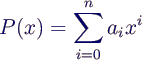
    • mit
    • 
  • Einsetzen der Punkte in die Polynomdefinition liefert m Gleichungen für die n+1 unbekannten Koeffizienten a_i
    • 
  • überbestimmtes lineares Gleichungssystem mit Vandermonde-Matrix
    • 
• Was kann schief gehen:
  • A hat nicht Rang n
    • zu wenig Daten
    • Daten sind nicht unabhängig (schlechtes Experiment!)
    • Modell passt nicht
  • Modell macht keinen Sinn
    • z.B. kein Polynom, sondern ganz anderer Zusammenhang
    • Ausgleichsrechnung liefert gut aussehende Kurve
    • Extrapolation oder Interpolation ergibt trotzdem unsinnige Werte
    • Modell kommt aus der Theorie oder Erfahrung, Mathematik kann da nicht helfen!
• Matlabfunktionen
  • QR-Zerlegung der Matrix A
    • [Q, R] = qr(A)
  • Lösung des linearen Ausgleichsproblems A x ≈ b
    • x = A \ b
  • Ausgleichspolynom n-ter Ordnung zu Datenpunkten xi, yi
    • poly = polyfit(xi, yi, n)
  • Anwenden des Polynoms auf Werte x
    • y = polyval(poly, x)
• Messwerte mit verschiedener Genauigkeit:
  • gegeben seinen m Messwerte
    • (xi, yi), i = 1, .. m, mit xi ≠ xj für i ≠ j
    • jeder mit einer Genauigkeit σ_i für yi
  • Die Koeffizienten a_i des Fit-Polynoms n-ten Grades erhält man durch Lösung des Ausgleichsproblems
    • 
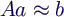
    • mit
    • 
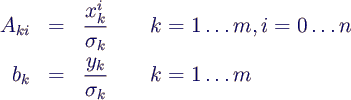
    • Beweis: [6]
  • Statt Polynomen kann man auch beliebige andere Grundfunktionen verwenden:
    • 
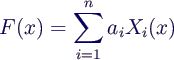
    • Polynom wäre dann der Spezialfall
    • X_i(x) = x^i-1
• Aufgaben:
  • Aufgabe 11
  • Aufgabe 12