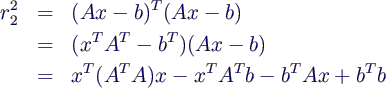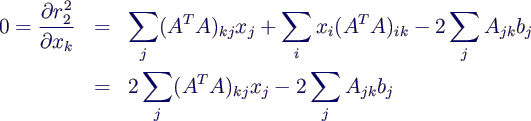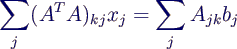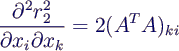Herleitung der Normalengleichung

• Sei A eine mxn-Matrix (m > n) von maximalem Rang n, b ein m-Vektor. Dann gibt es genau einen n-Vektor x, der den quadratischen Fehler r₂ des linearen Gleichungssystem
  • A x = b
• minimiert. Er ist gegeben als Lösung der Normalengleichung
  • (A^T A) x = A^T b
• Beweis:
  • Statt r₂ kann man auch r₂² minimieren. Es gilt
    • 
  • in Komponenten
    • 
  • Notwendige Bedingung für ein Minimum ist, dass die Ableitung verschwindet, also
    • 
  • wobei der letzte Schritt aus der Symmetrie von A^T A folgt:
    • 
  • Man erhält also
    • 
  • bzw. in Matrix-Schreibweise
    • (A^T A) x = A^T b
  • Hinreichende Bedingung für ein Minimum ist die positive Definitheit der 2. Ableitung. Nun ist
    • 
  • Die Matrix A^T A ist aber positiv definit, da sie positiv ist und maximalen Rang n hat.