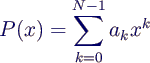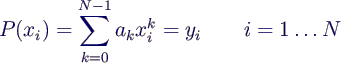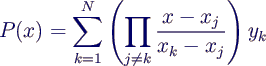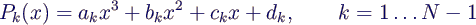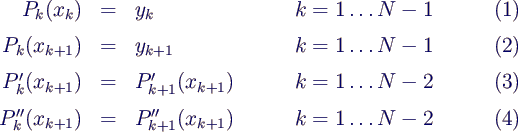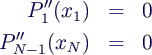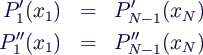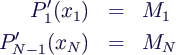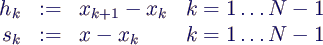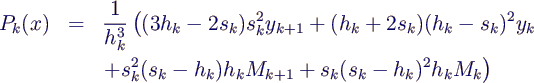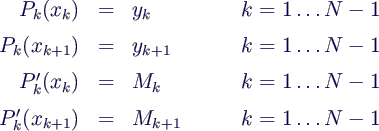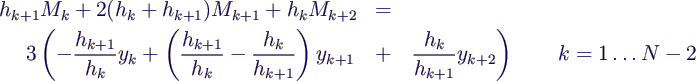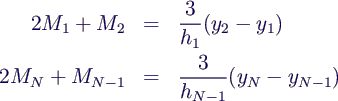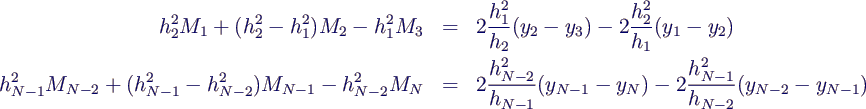Interpolation

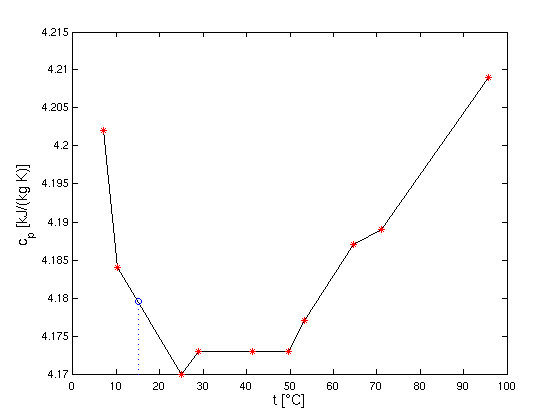
• Spezifische Wärmekapazität c_p von Wasser:
  • einige Messwerte wurden bestimmt
  • daraus soll Wert für t₁ = 15 °C ermittelt werden
  • am einfachsten: lineare Interpolation
    • 
  • Ergebnis: c_p(t₁) = 4.1795 kJ/(kg K)
  • kann man einen "besseren" Wert bekommen?
• Problem der Interpolation:
  • gegeben N Punkte
    • (x_i, y_i), i = 1, .. N, mit x_i ≠ x_j für i ≠ j
  • gesucht Funktion f einer vorgegebenen Klasse (z. B. Polynom) mit
    • f(x_i) = y_i, i = 1, .. N
• Polynom-Interpolation:
  • Es gibt genau ein Interpolationspolynom P vom Grad N-1
    • 
  • Einsetzen der Punkte liefert N Gleichungen für die N Koeffizienten a_k
    • 
  • in Matrixform
    • 
  • Systemmatrix
    • Vandermonde-Matrix
    • nicht singulär (bei x_i ≠ x_j für i ≠ j)
    • schlechte Kondition bei kleinen Abständen zwischen den x_i
• Lagrangeform der Lösung:
  • Lösung direkt hinschreibbar, etwa quadratisches Polynom für N = 3
    • 
  • Überprüfen durch Einsetzen von x₁, x₂, x₃
  • allgemein
    • 
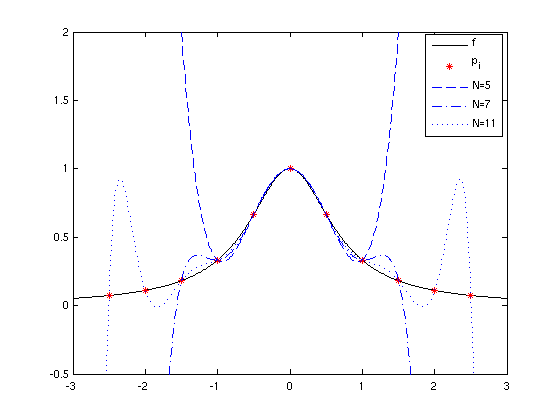
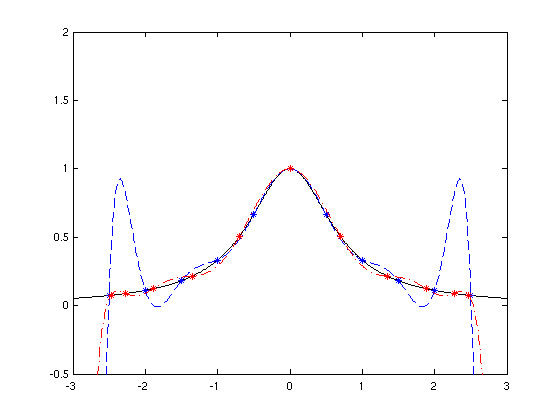
• Beispiele:
  • "sinnvoll" nur bei kleinem N
    • 
  • starke Überschwinger bei großem N
    • 
  • bei bekannter Funktion f optimierbar durch geschickte Wahl der Stützstellen x_i (Tschebycheff-Knoten)
    • 
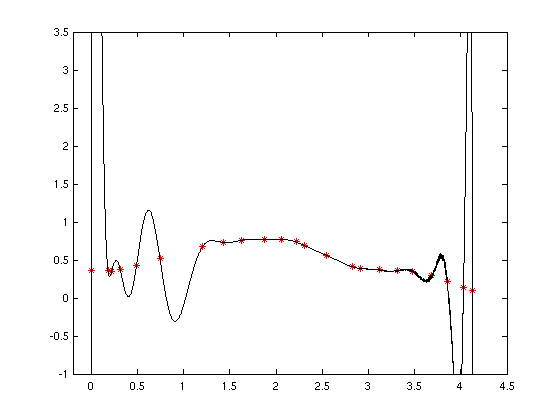
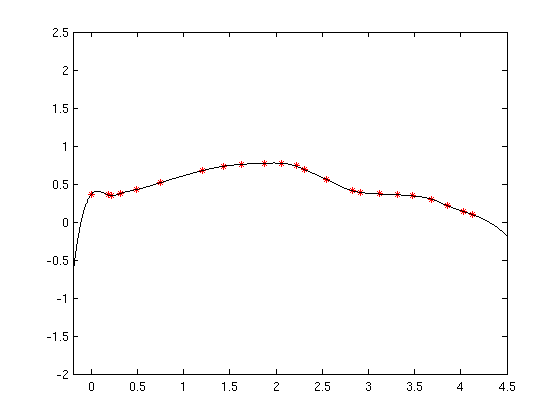
• Kubische Splines:
  • Alternative: stückweise Polynome P_k(x) niedriger Ordnung
  • kubische Splines definiert durch
    • Polynom 3. Ordnung zwischen je zwei aufeinanderfolgenden Punkten
    • 1. und 2. Ableitungen sind stetig
  • Beispiel
    • 
  • Splines gegeben durch je 4 Koeffizienten a_k, b_k, c_k, d_k
    • 
  • Bedingungen
    • 
  • Anzahl der Koeffizienten: 4N - 4
  • Anzahl der Bedingungen: (N-1) + (N-1) + (N-2) + (N-2) = 4N-6
  • bleibt je eine zusätzliche Bedingung an den Endpunkten x₁, x_N
• Wahl der Randbedingungen:
  • natürliche Splines
    • Extrapolationen (Kurven außerhalb [x₁ x_N]) verlaufen linear
    • 
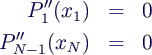
  • "not-a-knot"-Splines
    • bei x₂ und x_N-1 dreimal stetig differenzierbar
    • 
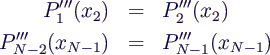
    • ein einziges kubisches Polynom durch (x₁, x₂, x₃) bzw. (x_N-2, x_N-1, x_N)
  • periodische Splines
    • 
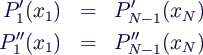
    • wichtig bei geschlossenen Kurven
  • Ableitungen M₁, M_N an den Endpunkten bekannt
    • 
• Bestimmung der Koeffizienten:
  • die (noch unbekannten!) Steigungen an den Punkten seien M_k, also
    • 
  • mit den Abkürzungen
    • 
  • hat das Polynom
    • 
  • die Eigenschaften
    • 
  • aus der Stetigkeit der 2. Ableitung (4) erhält man N-2 lineare Gleichungen für die M_k
    • 
  • 2 ergänzende Gleichungen für natürliche Splines
    • 
  • 2 ergänzende Gleichungen für "not-a-knot"-Splines
    • 
  • Details der Rechnung im Anhang
• Matlab-Funktionen:
  • Interpolation bei Punkten x, y, an den Stellen xi
    • yi = interp1(x, y, xi, Methode)
    • Methoden (u.a.) "linear", "spline"
    • "spline" verwendet not-a-knot-Randbedingungen
  • Interpolationspolynom bestimmen
    • poly = polyfit(x, y, length(x)-1);
  • Zwischenwerte des Polynoms berechnen
    • yi = polyval(poly, xi);
• B-Splines:
  • interpolieren beliebige Raumkurve
  • zusätzliche Kontrollpunkte legen Tangentenrichtungen fest
  • Basis von Freiformkurven in 2D-CAD
  • Verallgemeinerung auf Flächen
    • NURBS (Non Uniform Rational B-Splines)
    • Basis von Freiformflächen in 3D-CAD
• Aufgaben:
  • Aufgabe 9
  • Aufgabe 10