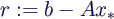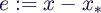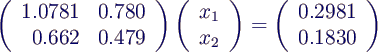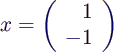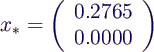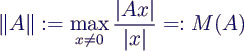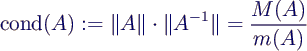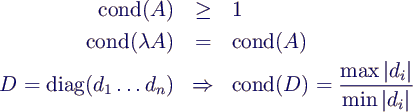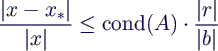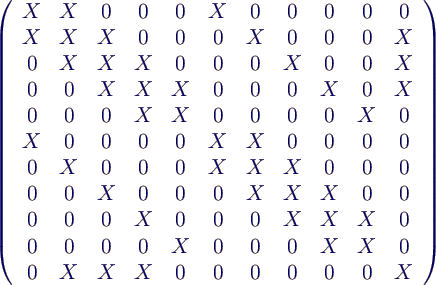Lineare Gleichungssysteme
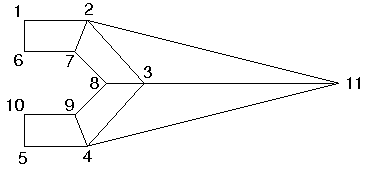
- Berechnung eines idealen Fachwerks:
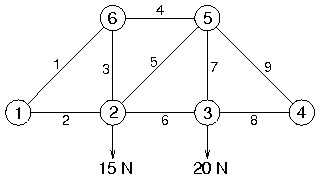
- Beispiel mit 6 Gelenken und 9 Stäben
- 3 Auflagekräfte für statische Bestimmtheit
- Gelenk 1 horizontal und vertikal fixiert
- Gelenk 4 vertikal fixiert
- an jedem Gelenk Kräftegleichgewicht (2-dim), daher
mit α = 1/
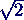
- ergibt lineares Gleichungssystem mit 9 Gleichungen
für 9 Unbekannte
- Existenz und Eindeutigkeit von Lösungen:
- Sei A eine n x n-Matrix, b ein n-elementiger
Spaltenvektor. Das lineare Gleichungssystem
- ist genau dann lösbar, wenn
- Die Lösung ist genau dann eindeutig, wenn A nicht
singulär ist (d.h. rang(A) = n oder äquivalent det(A) ≠ 0)
- Beweis: Jedes Buch über lineare Algebra.
- Gaußscher Algorithmus:
- Beispielsystem
- 1. Schritt: x1 eliminieren in 2. und 3.
Gleichung. Koeffizient von x1 ist das 1. Pivot-Element. 1.
Gleichung mit 1/2 multiplizieren und
von 2. Gleichung subtrahieren, dann 1. Gleichung mit (-3/2) multiplizieren und von der 3. Gleichung
subtrahieren. Ergebnis:
- 2. Schritt: x2 eliminieren in 3.
Gleichung.Koeffizient von x2 ist das 2. Pivot-Element. 2.
Gleichung mit 7/5 multiplizieren und
von 3. Gleichung subtrahieren. Ergebnis:
- Aufgrund der Dreiecksgestalt der Matrix kann das
System nun von unten nach oben gelöst werden (Rückwärtssubstitution)
- in 2. Gleichung einsetzen
- in 1. Gleichung einsetzen
- Einsetzen der Lösung in das ursprüngliche System
verifiziert das Ergebnis.
- LU-Zerlegung:
- obere Dreiecksmatrix vor der Rückwärtssubstitution
- untere Dreiecksmatrix aus den Vorfaktoren beim
Eliminieren, mit 1 in der Diagonalen
- dann gilt (nachrechnen!)
- das klappt immer (bis auf Vertauschungen, s. u.)!
Beweis z.B. [3]
- Mit dieser Zerlegung schnelle Lösung für andere
rechte Seiten
- Löse
- L y = c
- (y1 = c1, in Gleichung
für y2 einsetzen ergibt y2, ...
(Vorwärtssubstitution))
- Löse durch Rückwärtssubstitution
- Dann löst x die Ausgangsgleichung
- Falls A symmetrisch und positiv (d.h. (x, Ax) >= 0),
kann auch die LU-Zerlegung symmetrisch gemacht werden
- A = L LT (Cholesky-Zerlegung)
- Zahl der Schritte
- berücksichtigt werden +, - * / als jeweils ein
Schritt
- Eliminieren der 1. Variablen
- N Multiplikationen und N Additionen pro
Gleichung
- zusammen also 2 N (N-1)
- analog für die folgenden Variablen, insgesamt also
- Rückwärtssubstitution
- Vorwärtssubstitution analog, aber N Multiplikationen
weniger wegen Faktor 1 in der Diagonalen, somit
- Was kann schiefgehen:
- Pivot-Element kann 0 sein oder zumindest sehr
klein
- Beispiel [1, S.58ff]
- exakte Lösung ist (nachrechnen!)
- Rechnung auf 5 signifikante Stellen
- x1 eliminieren
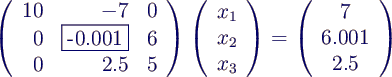
- x2 eliminieren (immer auf 5
signifikante Stellen runden!)
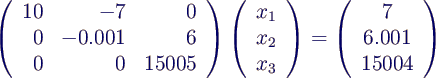
- Rückwärtssubstitution
- Ursache: kleiner Pivot-Wert 0.001
- Pivotisierung:
- Lösung: vertausche Gleichungen oder Variablen oder
beides, so dass Pivot-Element betragsmäßig möglichst groß
- übliches Vorgehen: Gleichungen vertauschen, so dass
betragsmäßig größtes Element der Spalte nach oben kommt (Spalten- oder partielle
Pivotisierung)
- im Beispiel
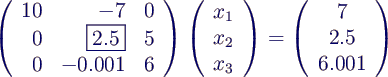
- x2 eliminieren
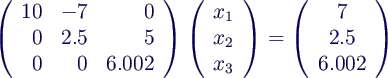
- Rückwärtssubstitution
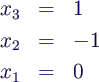
- bei LU-Zerlegung muss die Vertauschung durch eine
Permutationsmatrix P berücksichtigt werden
- P bewirkt eine Vertauschung der Zeilen von A
- bei mehrfachen Vertauschungen P1,
P2, ..., Pn ergibt sich P als Produkt
- im Beispiel Vertauschung von Zeile 2 und 3
- man liest aus der Rechnung ab
- wobei auch die Werte in L aus früheren Schritten
entsprechend vertauscht werden müssen
- damit gilt (nachrechnen!)
- Rundungsfehler:
- Unterschied zwischen exakter Lösung x und
berechneter Lösung
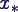 durch
Runden
durch
Runden
- Residuum
- Fehler
- Beispiel
- exakte Lösung
- Lösung bei Rechnung mit 4 signifikanten Stellen (in
jedem Schritt runden!)
- Residuum
- aber Fehler
- Das Residuum ist beim Gaußalgorithmus mit
Spalten-Pivotisierung immer klein (Details in [1] und [8]).
- Norm und Kondition einer Matrix
- Fehler bei linearem Gleichungssystem wächst mit
"Größe" von A, etwa bei Multiplikation des Systems mit einem großen
Faktor
- "Größe von A" wird präzisiert als Norm von A
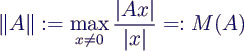
- maximal möglicher Streckungsfaktor M(A) eines
Vektors
- minimaler Streckungsfaktor analog

- für nicht-singuläres A, sonst 0
- Veranschaulichung
- 2x2-Matrix bildet Einheitsvektoren auf
(verdrehte) Ellipse ab
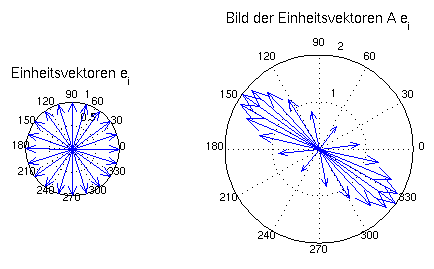
- M(A) bzw. m(A) = größte bzw. kleinste Halbachse
- mehrdimensional analog (Ellipsoid)
- Konditionszahl einer nicht-singulären Matrix
- Eigenschaften der Konditionszahl
- Ist cond(A) groß, so ist A "fast singulär".
- Fehler im Ergebnis wächst mit cond(A) - unabhängig
vom Algorithmus!
- allgemein gilt
- Faustregel
- Jeder Faktor 10 in cond(A) kostet eine
signifikante Stelle im Ergebnis.
- obige 2d-Beispielmatrix hatte
- Matlab-Routinen:
- direktes Auflösen eines linearen Gleichungssystems
(über LU-Zerlegung)
- explizite LU-Zerlegung
- Cholesky-Zerlegung für positives A
- Vorwärts-/Rückwärtssubstitution automatisch bei
x = A \ b und A Dreiecksmatrix
- Konditionszahl
- cond(A) genau, aber
aufwändig
- condest(A) schneller
Schätzwert
- Dünnbesetzte Matrix (sparse
matrix)
- Matrix, deren meisten Elemente 0 sind
- Beispiel FEM
- Systemmatrix
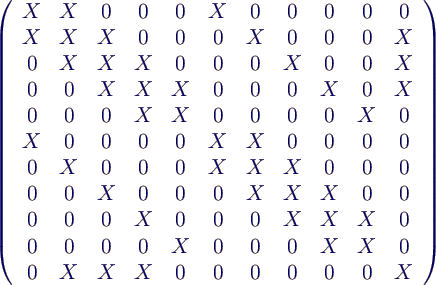
- Probleme mit Speicherplatz und
Standardalgorithmen
- spezielle iterative Verfahren
- wichtig u.a. für Solver von partiellen
Differentialgleichung (FEM, Strömungen etc.)
- ausgiebige Spezialliteratur, vgl. [11]
- Aufgaben:



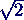
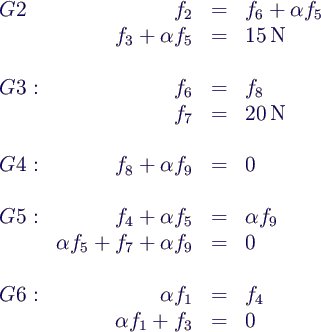
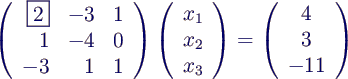
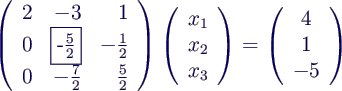
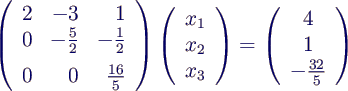
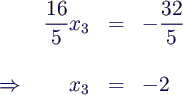
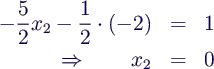
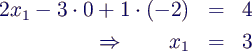
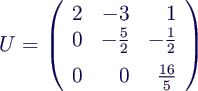
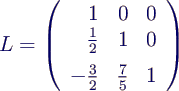
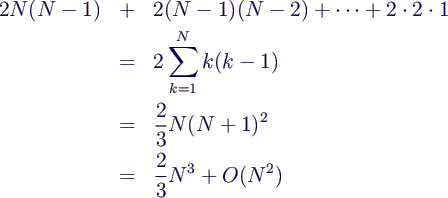
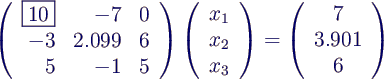
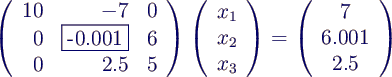
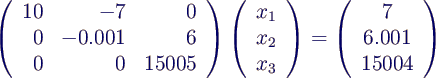
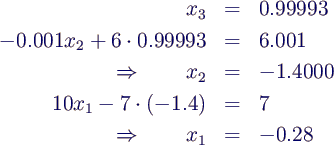
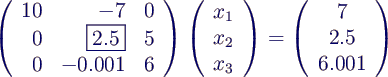
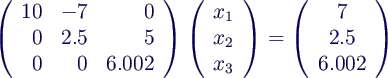
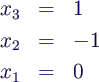
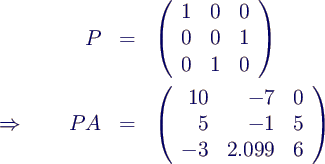

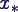 durch
Runden
durch
Runden