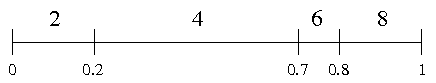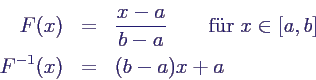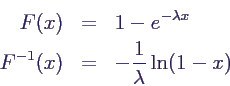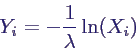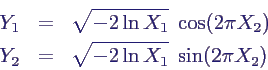Zufallszahlen mit vorgegebener Verteilung

• Aufgabenstellung:
  • berechne Zufallszahlenfolge Y_i mit gegebener (diskreter oder kontinuierlicher) Verteilungsfunktion
  • genauer: berechnete Folge verhält sich bei (vielen) statistischen Tests wie entsprechend verteilte Zufallsgröße
  • Startpunkt immer berechnete Zufallszahlen X_i ~ U(0,1)
• Grundidee bei diskreter Verteilung:
  • gegeben sei Wahrscheinlichkeitsverteilung p_k = P(Y = a_k)
  • zerlege Intervall [0,1] in Strecken I_k der Länge p_k
    • bestimme Wert von X_i ~ U(0,1)
    • 
  • Beispiel
    • a_i = (2, 4, 6, 8), p_i = (0.2, 0.5, 0.1, 0.2)
    • 
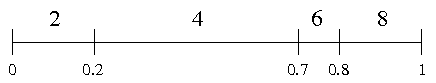
  • Streckenaufteilung geht direkt mit der kumulativen Verteilungsfunktion F(a) = P(X ≤ a)
    • 
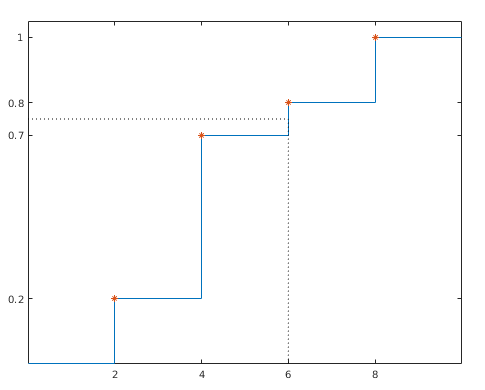
    • damit: Y_i = F^-1(X_i)
• Implementation in Matlab:
  • Definition der Verteilung
    • a = [2, 4, 6, 8];
      p = [0.2, 0.5, 0.1, 0.2];
      F = cumsum(p)     % -> [0.2, 0.7, 0.8, 1.0]
  • berechnen von Y
    • X = rand
      idx = find(F>X, 1)
      Y = a(idx)
  • find klappt nicht ganz so einfach für X Vektor
    • quick and dirty: Schleife
    • Verteilung damit bei 100 Werten
    • 
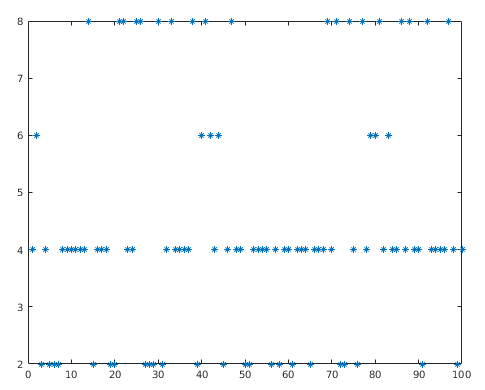
  • erhaltene Anzahlen

    • 2	4	6	8
      24	50	7	19

    • ist das ok? vgl. Testtheorie
• Verbesserungen:
  • Grundverfahren aufwändig
  • Trick für Gleichverteilung in n:m
    • Y_i = floor(n + (m - n + 1) X_i)
  • Trick für Bernoulli
    • X_i ≤ p → Y_i = 1, sonst 0
    • entspricht Grundverfahren
  • Trick für Binomial-Verteilung B(n,p)
    • mache n Bernoulli-Würfe Z_k, k = 1..n
    • Y_i = Z₁ + ... + Z_n
• Grundidee bei stetiger Verteilung:
  • Ausgangspunkt Verteilungsfunktion F(y) = P(Y ≤ y)
  • inverse Transformation (wie bei diskreter Verteilung)
    • Y_i = F^-1(X_i)
  • prima, wenn F^-1 explizit berechenbar
  • Gleichverteilung U(a,b)
    • 
  • Exponentielle Verteilung Ex(λ)
    • 
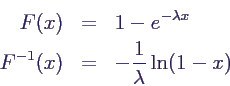
    • kleine Vereinfachung, da auch 1 - X_i ~ U(0,1)
    • 
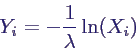
• Normalverteilung:
  • Berechnung von F^-1 nur numerisch, zu aufwändig
  • es genügt Y ~ N(0,1), denn damit
    • Z = μ + σ Y ~ N(μ, σ²)
  • Box-Muller-Algorithmus
    • bestimme X₁, X₂ ~ U(0,1), damit
    • 
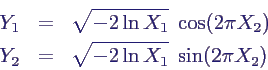
  • Y₁, Y₂ ~ N(0,1), unabhängig
  • Beweisidee:
    • betrachte 2d-Normalverteilung
    • gehe zu Polarkoordinaten über
  • Details im Anhang
• Alternative Zikkurat-Verfahren:
  • heute verbreitet, weil schneller
  • geht grundsätzlich für beliebige Verteilungen
  • Grundidee
    • überdecke Fläche unter dem Graphen der Dichtefunktion mit gleichverteilten Zufallspunkten
    • wähle einen Punkt und gebe die x-Koordinate aus
  • praktische Umsetzung
    • würfle Punkt auf der Ebene in geeignetem Bereich
    • teste, ob er unterhalb des Graphen der Dichtefunktion liegt
    • ja: gib x-Wert zurück, nein: verwirf den Punkt
  • Problem: x-Werte gehen grundsätzlich bis unendlich
  • Verbesserung (weniger verworfene Punkte)
    • überdecke Graphen mit N-1 Rechtecken und einem Endstück jeweils gleicher Fläche
    • 
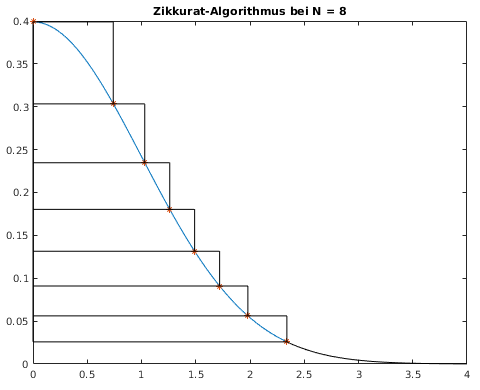
    • würfle Nummer 1 .. N und einen Punkt im Rechteck
    • besondere Behandlung für das unterste Stück
• Aufgaben:
  • Aufgabe 20
  • Aufgabe 21