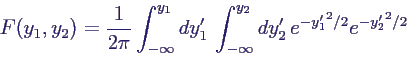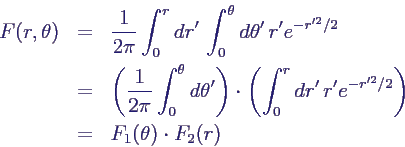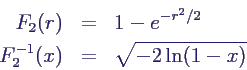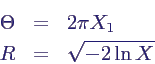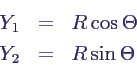Herleitung des Box-Muller-Verfahrens

• Trick:
  • berechne statt eines Zufallswerts gleich zwei auf einmal
  • betrachte dazu zwei unabhängige Zufallsvariablen Y₁, Y₂ ~ N(0,1)
• Die gemeinsame Verteilungsfunktion lautet
  • 
• Zur Berechnung führt man Polarkoordinaten ein
  • 
• und erhält als transformiertes Volumen-Element (Jacobi-Matrix nachrechnen!)
  • dy₁ dy₂ = r dr dθ
• Das Integral wird dann
  • 
• Dies ist die Verteilungsfuntion zweier unabhängiger Zufallsvariablen Θ und R, wobei Θ gleichverteilt ist in [0, 2π].
• Die Verteilungsfunktion von R und ihr Inverses berechnet man leicht zu
  • 
• Benutzt man noch, dass mit X ~ U(0,1) auch 1 - X ~ U(0,1), kann man also folgendermaßen vorgehen:
  1. bestimme X₁, X₂ ~ U(0,1)
  2. berechne daraus
     • 
  3. und damit
     •