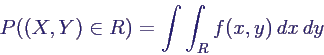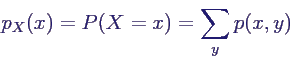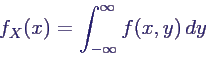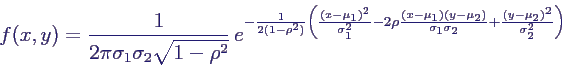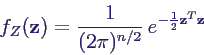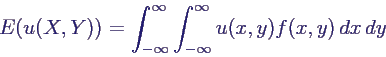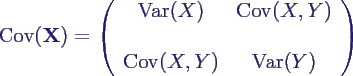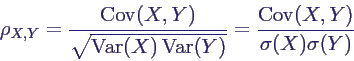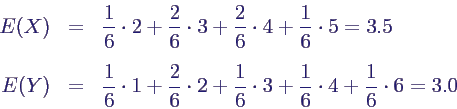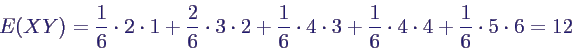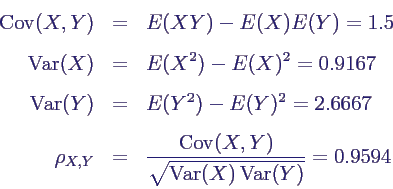Zufallsvektoren

• Definition von Zufallsvektoren:
  • häufig interessieren mehrere Zufallsvariablen gleichzeitig
    • verschiedene Merkmale (Größe, Gewicht, Alter)
    • Lebensdauern verschiedener Teilkomponenten
    • Ergebnisse wiederholter Messungen
  • formal
    • Sei (Ω, ℱ, P) ein Wahrscheinlichkeitsraum. Ein n-dimensionaler Zufallsvektor X = (X₁, X₂, ..., X_n) ist eine Abbildung X: Ω → ℝⁿ, wobei für jedes (a₁, ..., a_n) ∈ ℝⁿ
    • 
  • i. F. häufig nur für n=2 formuliert
    • Bezeichnung X = (X, Y)
    • Verallgemeinerung meistens klar
• Verteilungsfunktionen:
  • für diskrete Zufallsvariable X = (X, Y)
    • gemeinsame Wahrscheinlichkeitsfunktion p(x,y) mit
    • p(x,y) = P(X = x, Y = y)
  • für stetige Zufallsvariable X = (X, Y)
    • gemeinsame Dichtefunktion f(x,y) mit
    • 
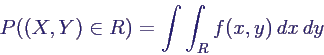
    • für Rechteck R ⊂ ℝ²
  • in beiden Fällen
    • (kumulative) Verteilungsfunktion F(x,y)
    • F(x,y) = P(X ≤ x, Y ≤ y)
• Rand- oder marginale Verteilungen:
  • Verteilung der einen Größe, unabhängig vom Wert der anderen
  • X diskret → marginale Wahrscheinlichkeitsfunktion p_X
    • 
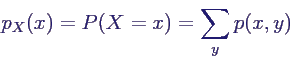
    • analog p_Y
  • X stetig → marginale Dichtefunktion f_X
    • 
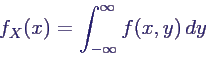
    • analog f_Y
  • X, Y unabhängig ⇔ P(X ≤ x, Y ≤ y) = P(X ≤ x) P(Y ≤ y)
  • äquivalent dazu:
    • p(x,y) = p_X(x) p_Y(y) (diskret)
    • f(x,y) = f_X(x) f_Y(y) (stetig)
  • Satz: X, Y unabhängig ⇒ E(X Y) = E(X) E(Y)
• Beispiel 3-2-Würfel:
  • Wurf mit zwei Würfeln A, B
    • A: je zweimal die Zahlen 1, 2, 3
    • B: je dreimal die Zahlen 1,2
  • Ergebnisraum
    • Ω = {(1,1), (1,2), (2,1), (2,2), (3,1), (3,2)}
    • alle ω mit p = 1/6
  • Zufallsvariable X = Summe der beiden Werte
    • mögliche Werte 2,3,4,5
  • Zufallsvariable Y = Produkt der beiden Werte
    • mögliche Werte 1,2,3,4,6
  • Tabelle der gemeinsamen Wahrscheinlichkeitsfunktion p(x,y)

    • X/Y	1	2	3	4	6
      2	1/6	0	0	0	0
      3	0	2/6	0	0	0
      4	0	0	1/6	1/6	0
      5	0	0	0	0	1/6

  • Randverteilungen durch Summe der Zeilen bzw. Spalten

    • X	2	3	4	5
      pX	1/6	2/6	2/6	1/6

    • Y	1	2	3	4	6
      pY	1/6	2/6	1/6	1/6	1/6

  • offensichtlich nicht unabhängig, z.B.
    • p(3,2) = 2/6 ≠ p_X(3) p_Y(2) = (2/6) · (2/6)
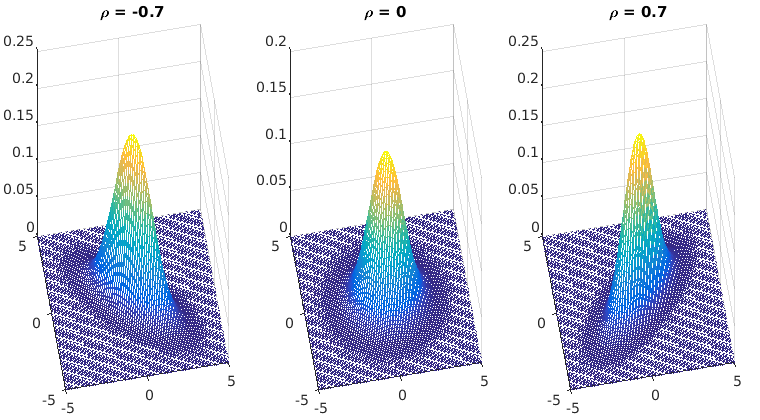
• Beispiel bivariate (zweidimensionale) Normalverteilung:
  • definiert durch gemeinsame Dichtefunktion
    • 
  • Parameter ρ: Korrelationskoeffizient, |ρ| < 1
  • Berechnung der Randverteilungen ⇒
    • X ~ N(μ₁, σ₁²), Y ~ N(μ₂, σ₂²) (nachrechnen!)
  • im Bild, für μ₁ = μ₂ = 0, σ₁ = σ₂ = 1
    • 
• Mehrdimensionale (multivariate) Normalverteilung:
  • n-dimensionale Standard-Normalverteilung mit z ∈ ℝⁿ
    • 
  • beliebige Normalverteilung durch lineare Transformation
    • X = A Z + μ
    • μ ∈ ℝⁿ, A nicht-singuläre nxn-Matrix
  • damit Dichtefunktion
    • 
  • mit Kovarianzmatrix
    • Σ = A A^T
• Kenngrößen von Zufallsvektoren:
  • Erwartungswert des Vektors ist einfach der Vektor der Einzelwerte
    • E(X) := (E(X), E(Y))
  • Erwartungswert einer Funktion u(X,Y) bei stetigem X = (X,Y)
    • 
  • Kovarianz zweier Zufallsvariablen
    • Cov(X,Y) := E((X - E(X)) (Y - E(Y)))
  • Eigenschaften der Kovarianz
    • Cov(X,Y) = Cov(Y,X)
    • Cov(X,X) = Var(X)
    • Cov(aX + b, Y) = a Cov(X, Y)
    • Cov(X,Y) = E(X Y) - E(X) E(Y)
    • Var(X + Y) = Var(X) + Var(Y) + 2 Cov(X,Y)
  • Kovarianz misst den Grad der linearen Abhängigkeit von X und Y
  • X, Y unkorreliert :⇔ Cov(X,Y) = 0
  • X, Y unabhängig ⇒ X, Y unkorreliert
    • Umkehrung gilt nicht!
• Kovarianzmatrix:
  • bei zwei Zufallsvariablen
    • 
  • bei n Zufallsvariablen
    • 
• Korrelationskoeffizient:
  • Cov(X,Y) ändert sich mit Skalierung, daher durch Skalengröße teilen
  • Definition des Korrelationskoeffizienten
    • 
  • Eigenschaften
    • |ρ_X,Y| ≤ 1
    • ρ_X,Y = 1 ⇔ X = aY + b mit a > 0
    • ρ_X,Y = -1 ⇔ X = aY + b mit a < 0
  • Stärke des linearen Zusammenhangs
• Kenngrößen im Beispiel 3-2-Würfel:
  • Erwartungswert direkt über die Randverteilungen
    • 
  • analog E(X²) und E(Y²) ergibt
    • E(X²) = 13.1667
    • E(Y²) = 11.6667
  • Berechnung von E(X Y) über die Tabelle von p(x,y)
    • 
  • damit
    • 
  • X und Y sind stark positiv korreliert (klar!)
• Kenngrößen der bivariaten Normalverteilung:
  • Randverteilungen X,Y (eindimensional) normalverteilt ⇒
    • E(X) = μ₁, E(Y) = μ₂
    • Var(X) = σ₁², Var(Y) = σ₂²
  • Berechnung von E(X Y) als Doppelintegral liefert (nachrechnen!)
    • E(X Y) = σ₁ σ₂ ρ + μ₁ μ₂
  • damit sofort
    • Cov(X,Y) = σ₁ σ₂ ρ
    • ρ_X,Y = ρ
  • ρ ist wirklich der Korrelationskoeffizient
  • hier gilt die Umkehrung: Cov(X,Y) = 0 ⇒ X, Y unabhängig
    • denn: ρ = 0 ⇒ f(x,y) = f_X(x) f_Y(y)
• Aufgaben:
  • Aufgabe 15