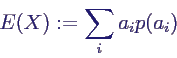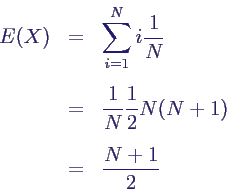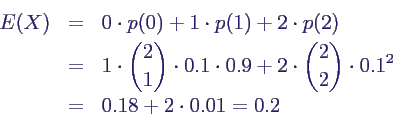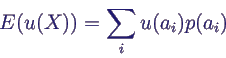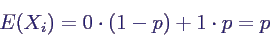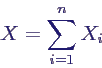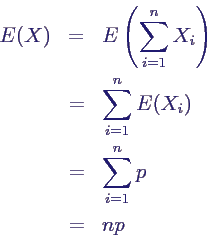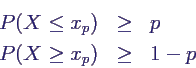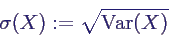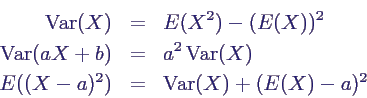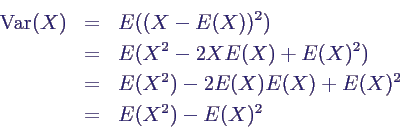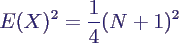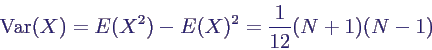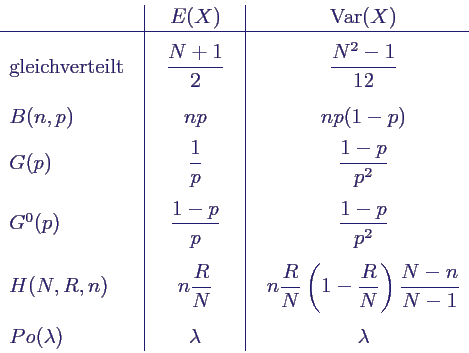Eigenschaften diskreter Verteilungen

• Erwartungswert einer diskreten Zufallsvariablen:
  • X diskrete Zufallsvariable mit Werten a_i und Wahrscheinlichkeitsfunktion p(a_i)
  • Erwartungswert E(X) (oder μ_X)
    • 
• Beispiele:
  • X Gleichverteilung bei Werten 1 ... N
    • 
  • X binomialverteilt nach B(2, 0.1)
    • 
  • X binomialverteilt nach B(n,p) → E(X) = n p
    • Berechnung im Anhang
• Eigenschaften des Erwartungswerts:
  • Transformation einer Zufallsvariable mit u: ℝ → ℝ
    • 
  • linear
    • E(aX) = a E(X)
    • E(X + Y) = E(X) + E(Y)
  • normiert
    • E(1) = 1
• Anwendung: Erwartungswert bei B(n,p):
  • Zufallsvariable X_i misst Erfolg bei i-tem Versuch
    • 
  • Erwartungswert von X_i
    • 
  • für X ~ B(n,p) ist
    • 
  • also Erwartungswert von X
    • 
• Quantile:
  • Für p ∈ [0,1] ist das p-Quantil von X ein Wert x_p mit
    • 
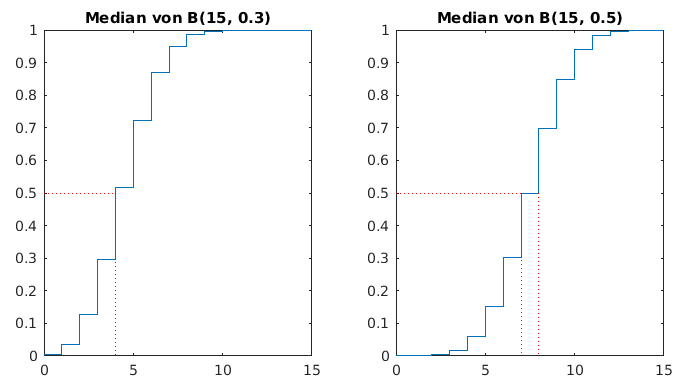
  • Das 0.5-Quantil heißt auch Median.
  • lässt sich aus der kumulativen Verteilungsfunktion F(x) ablesen
  • zwei Möglichkeiten
    • F(x) nimmt p nicht an ⇒ p-Quantil eindeutig
    • F(x) nimmt p an ⇒ jeder Wert aus Intervall ist p-Quantil
    • man definiert dann den linken Endpunkt
  • Beispiel Binomialverteilung
    • 
• Varianz und Standardabweichung:
  • Wie stark streuen die Werte (genauer: Realisierungen) einer Zufallsvariablen X um den Mittelwert?
  • Varianz
    • Var(X) := E((X - E(X))²)
  • Standardabweichung
    • 
• Eigenschaften der Varianz:
  • X Zufallsvariable, a, b, ∈ ℝ
    • 
  • Beweis der ersten Formel
    • 
  • andere ähnlich
• Berechnung der Varianz für X gleichverteilt mit Werten {1, ..., N}:
  • Berechnen zunächst E(X²)
    • 
  • Erwartungswert von X von oben liefert
    • 
  • damit erhält man
    • 
• Werte für Beispiel-Verteilungen:
  • 
• Aufgaben:
  • Aufgabe 9