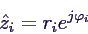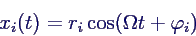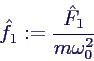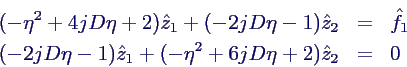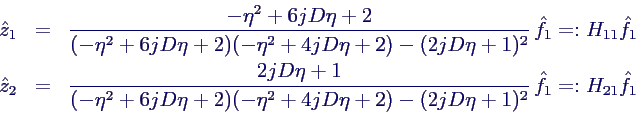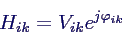Berücksichtigung der Dämpfung
- Standardbeispiel mit Anregung und Dämpfung:
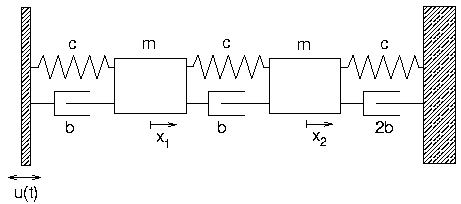
- Massen-Feder-Dämpfer-System wie vorher
- Fußpunkterregung
- Anregungskraft wirkt nur auf erste Masse
- mit
- verschiebe Zeitnullpunkt in Kraftmaximum →
ψ = 0
- Bewegungsgleichungen
- schreiben Erregerkraft als Realteil einer komplexen
Anregung
- und x = Re(z) für die komplexe Gleichung
- Ansatz
- ergibt lineares Gleichungssystem für
 i
i
- Auflösen liefert das Ergebnis für
 i, damit dann auch für
i, damit dann auch für
- Beispiel mit expliziten Werten:
- Zur Vereinfachung rechnen wir mit folgenden Werten
weiter
- Der Exponentialansatz liefert dann das
Gleichungssystem
- Auflösen ergibt
- in Polardarstellung umgerechnet
- Damit lautet die komplexe Lösung
- Die gesuchte relle Lösung ist dann der Realteil
- Vorgehen im allgemeinen Fall:
- Aufstellen der Bewegungsgleichung in Matrixform
- Lösen des Gleichungssystems für komplexe Amplituden

- komplexes
 in Polardarstellung bringen
in Polardarstellung bringen
- relle Lösung ist dann
- Standardbeispiel mit allgemeinen Werten:
- Einführung der üblichen Abkürzungen und
- ergibt
- Auflösen →
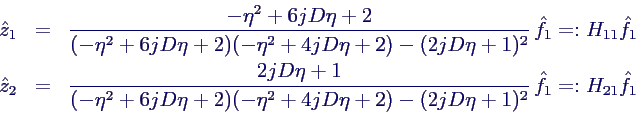
- mit komplexen Frequenzgang-Funktionen
H11, H21
- für gegebene Dämpfung D und Frequenzverhältnis η
= Ω/ω0 hat man
- komplexe Zahlen Hik
- Polardarstellung
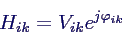
- Vergrößerungsfunktionen Vik
- Phasenverschiebungen φik
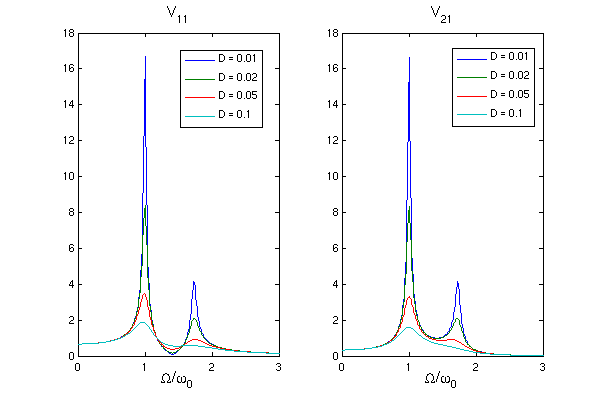
- graphisch
- Interpretation
- Resonanzen bei Eigenfrequenzen
ω0 und 1.73 ω0
- Resonanz bei ω0 ist stärker, da
sich bei kleinerer Frequenz die Dämpfung weniger auswirkt
- V11 hat keine Nullstelle → nur
partielle Schwingungstilgung
- Aufgaben:



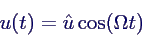

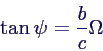
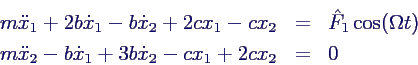
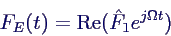
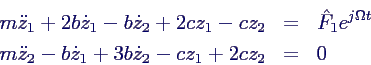
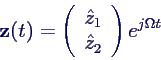
 i
i
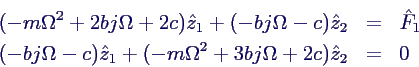
 i, damit dann auch für
i, damit dann auch für
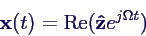
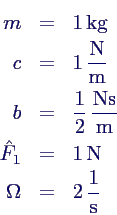
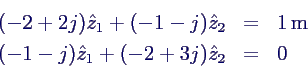
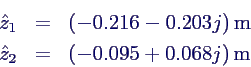

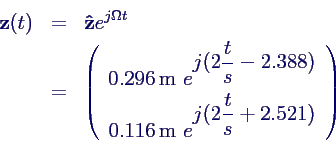
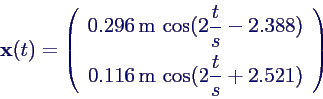
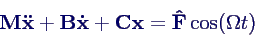


 in Polardarstellung bringen
in Polardarstellung bringen