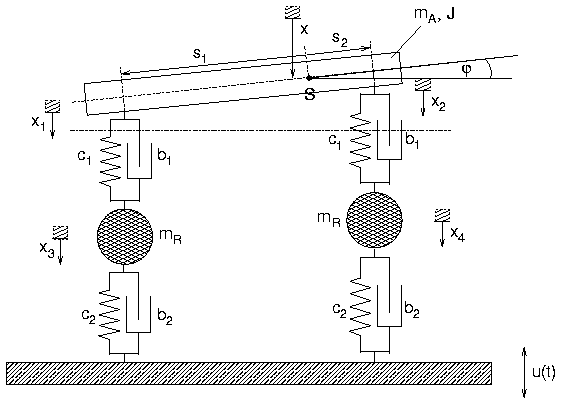
Aufgabe 16

• Ein Fahrzeug mit Radkästen und Stoßdämpfern werde durch das folgende System beschrieben:
  
  Eine Fahrt über eine unebene Fahrbahn bewirke eine Krafterregung mit der gleichen Funktion
  • F(t) = F₀ cos Ω t
• an beiden Rädern.
  1. Bestimmen Sie die Bewegungsgleichungen in Matrixform für die Koordinaten x, φ des Fahrgestells und x₃ und x₄ der Radkästen.
  2. Berechnen Sie die Eigenwerte und Modalmatrix für B = 0
  3. Transformieren Sie die Bewegungsgleichungen (incl. Dämpfung) mit dieser Modalmatrix. Was stellen Sie fest?
  4. Lösen Sie nun das gesamte System und berechnen Sie die Amplitude der Hub- und Nickschwingungen (in x und φ) des Fahrzeugs.
• Werte:
  • s₁ = 3 m, s₂ = 1 m
  • m_A = 800 kg, m_R = 30 kg, J = 900 kg m²
  • c₁ = 4 · 10⁵ N/m, c₂ = 10⁵ N/m
  • b₁ = 3200 Ns/m, b₂ = 800 Ns/m
  • F₀ = 500 N, Ω = 12 1/s
• Lösung