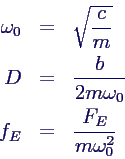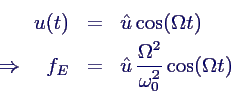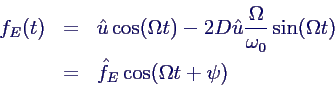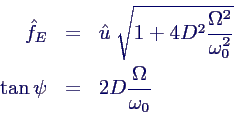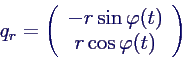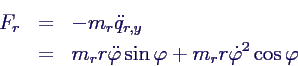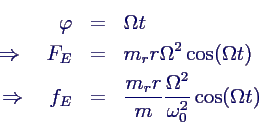Bestimmung der Differentialgleichung

• Erzwungene Schwingungen:
  • Anregung eines schwingfähiges System durch äußere Kräfte
  • Ursachen z.B.
    • direkte Kraftübertragung
    • Fußpunkterregung
    • Unwucht
  • Anregung häufig harmonische Schwingung
    • F_E(t) = 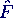_E cos(Ω t)
• Aufstellen der Bewegungsgleichung:
  • Schwinger mit viskoser Dämpfung
  • beliebige äußere Kraft F_E
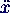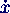    • m + b + c x = F_E
  • mit den Abkürzungen
    • 
  • ist dies
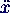    • + 2 D ω₀ 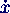+ ω₀² x = ω₀² f_E
• Erregerfunktion f_E:
  • gleiche Einheit wie x
  • im statischen Fall f_E(t) ≡ x_S = const:
    • x = x_S (statische Verschiebung)
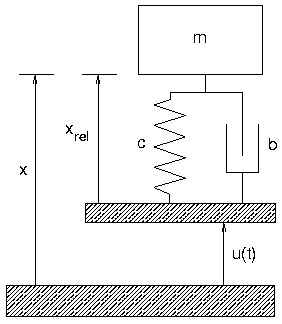
• Schwinger mit Fußpunkterregung:
  • System schwingt, weil sich der Boden bewegt
    
  • Bewegung des Bodens: u(t)
  • Abstand des Schwingers vom Boden
    • x_rel(t) = x(t) - u(t)
  • Dämpfung und Feder bezogen auf x_rel, daher
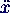    • + 2 D ω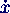₀ ( - ) + ω₀² (x - u) = 0
  • Bewegungsgleichung für x_rel
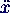    • _rel + 2 D ω_{0 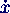rel} + ω₀² x_rel = - ≡ ω₀² f_E
  • speziell für harmonische Anregung
    • 
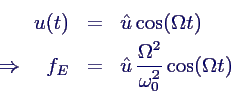
    • zusätzlicher Faktor Ω²
  • Bewegungsgleichung für x
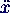    • + 2 D ω₀ 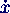+ ω₀² x = 2 D ω₀ + ω₀² u ≡ ω₀² f_E
  • für harmonische Anregung
    • 
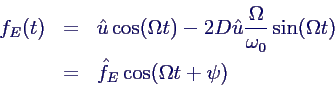
    • mit
    • 
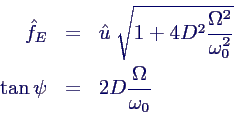
    • komplizierter Faktor und zusätzliche Phasenverschiebung ψ
• Vergleich der Bezugssysteme
  • Absolutsystem x
    • Inertialsystem
    • Kräfte leicht berechenbar
    • besser verallgemeinerbar auf gekoppelte Systeme
  • Relativsystem x_rel
    • x_rel leichter messbar
    • Abstand zum Boden wichtige Größe
    • keine zusätzliche Phasenverschiebung
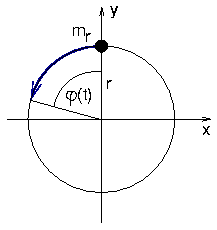
• Schwinger mit rotierender Unwucht:
  • Modell:
    • Masse m_r (Unwucht) rotiert im Abstand r von Drehachse
    • beliebige Drehbewegung φ(t)
    • Anregung des Schwingers (Gesamtmasse m) nur in vertikaler Richtung
      
  • Rotorbewegung q_r:
    • 
  • Vertikale Kraft durch Rotor auf Maschine = Gegenkraft zur Beschleunigung des Rotors
    • 
  • speziell bei konstanter Drehgeschwindigkeit
    • 
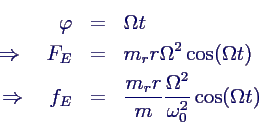
    • ebenfalls zusätzlicher Faktor Ω²
• Aufgaben:
  • Aufgabe 18