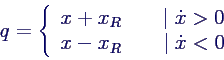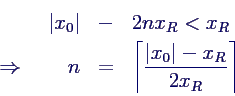Freie Schwingung mit Gleitreibung

• Feder-Masse-System:
  • mit Gleitreibung
    
  • als Applet zum Experimentieren
    • (Ortsraum)
    • (Phasenraum)
  • Bewegungsgleichung
    • 
  • in Standardform
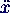    • + ω₀² x = - ω₀² x_R sign()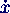
    • mit
    • 
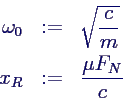
• Lösung der Bewegungsgleichung:
  • innerhalb eines Bereichs (v > 0 bzw. v < 0)
    • konstante Zusatzkraft
    • analog zur Gewichtskraft beim senkrechtem Pendel
    • effektive Verschiebung des Nullpunkts
  • Lösung durch Einführung der verschobenen Auslenkung
    • 
  • ergibt harmonische Schwingungsgleichung für q
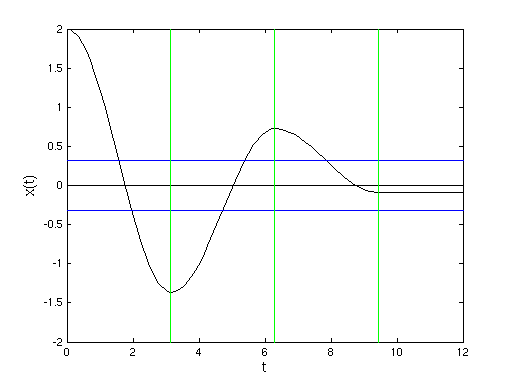
• Bewegung im Ortsraum:
  • 
  • gleiche Schwingungsperiode wie ohne Reibung
  • Nullpunkt wechselt bei jedem Bereichswechsel
  • Abnahme der Amplitude bei jeder Halbschwingung um 2 x_R
  • Reibung größer als Federkraft → Stillstand am Wendepunkt mit |x| < x_R
  • Zahl der Halb-Schwingungen: kleinste ganze Zahl mit
    • 
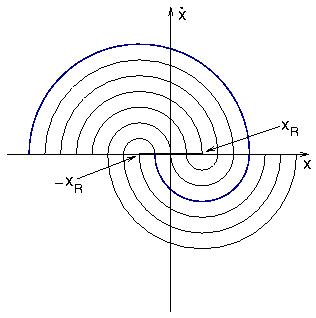
• Phasenraum-Diagramm:
  • 
  • Halbkreise mit verschiedenem Mittelpunkt in oberer und unterer Halbebene
  • endet in Strecke [-x_R,x_R] auf der x-Achse
• Aufgaben:
  • Aufgabe 17