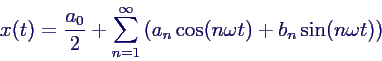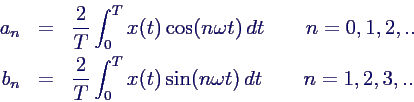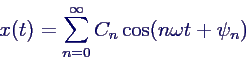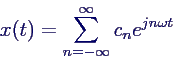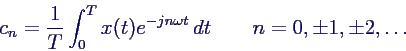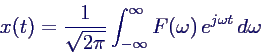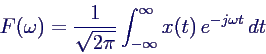Spektralanalyse

• Grundtatsache:
  • Periodische Funktionen können geschrieben werden als Überlagerung eines Grundtons (harmonische Funktion gleicher Frequenz) und seiner Obertöne (harmonische Funktionen mit n-facher Frequenz, n = 2, 3, 4, ..)
• Beispiel Sägezahnschwingung:
  • x(t) = t/2 für t = -π .. π
    
  • Aufbau aus Grund- und Oberschwingungen
    
  • als Applet zum Experimentieren
    • 
  • in Formeln:
    • x(t) = sin(t) - 1/2 sin(2t) + 1/3 sin(3t) - 1/4 sin(4t) ...
• Allgemeine Fourierzerlegung:
  • für ungerade Funktion x_u(t) (d.h. punktsymmetrisch am Ursprung) mit Periode T = 2π/ω
    • x_u(t) = b₁ sin(ω t) + b₂ sin(2ω t) + b₃ sin(3ω t) + b₄ sin(4ω t) + ...
  • analog für gerade Funktion x_g(t) (spiegelsymmetrisch zur y-Achse)
    • x_g(t) = a₀/2 + a₁ cos(ω t) + a₂ cos(2ω t) + a₃ cos(3ω t) + a₄ cos(4ω t) + ...
    • 
  • unsymmetrische Funktionen: Summe aus geradem und ungeraden Anteil
    • 
  • Berechnung der Koeffizienten mit folgenden Formeln
    • 
  • Alternativ mit Amplitude und Phasenverschiebung
    • 
• Spektrum:
  • Darstellung der Größe der Koeffizienten über der Frequenz
  • bei der Sägezahnschwingung
    
  • Spektren einiger Beispielfunktionen im Applet
    • 
• Komplexe Fourierzerlegung:
  • Zusammenfassung beider Summen mit einer komplexen e-Funktion
    • 
  • Zerlegung in Real- und Imaginärteil ergibt beide Teilreihen
  • Ausnutzung der Symmetrie von sin und cos → Werte für n und -n ergeben einfach Faktor 2
  • Berechnung der Koeffizienten c_n
    • 
  • Bestimmung von a_n und b_n aus c_n
    • a_n = c_n + c_-n
    • b_n = j (c_n - c_-n)
• Fouriertransformation:
  • Zerlegung einer nichtperiodischen Funktion in harmonische Funktionen
  • keine Periode → "alle" Frequenzen treten auf (nicht nur Obertöne)
  • Summe über Obertöne → Integral über alle Frequenzen ω
  • Koeffizienten c_n → komplexe Funktion F(ω) (Fouriertransformierte)
  • Darstellung der Funktion x(t)
    • 
  • Berechnung der Fouriertransformierten
    • 
• Spektralfunktion:
  • Stärke der Anteile zur Frequenz ω
  • je nach Fragestellung Re(F) oder |F|²
• Spektralanalyse in der Praxis
  • wichtige Methode zur Analyse von Schwingungen
  • spezielle numerische Methoden zur Berechnung der Fouriertransformierten (FFT = Fast Fourier Transform)
  • Geräte zur sofortigen Berechnung und Darstellung von Spektralfunktionen (Spektralanalysatoren)
• Beispiel:
  • seltsame Störungen in einer Maschine, hervorgerufen durch Vibrationen unbekannter Herkunft
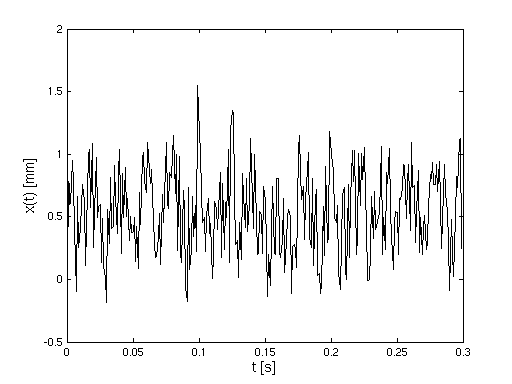
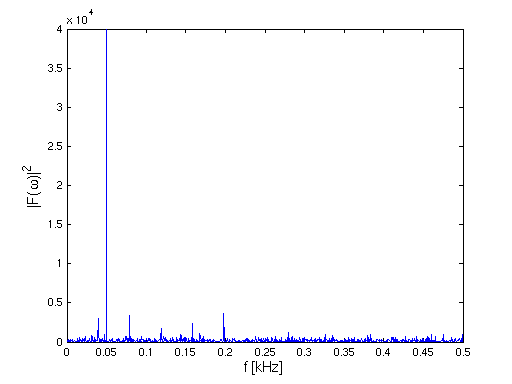
  • Messung der Vibrationen ergibt
    
  • Spektralanalysator zeigt
    • Untergrund bei allen Frequenzen
    • Spitzen in festen Frequenzabständen (Grundfrequenz 39.6 Hz)
    • zusätzliche Spitze bei 50 Hz
      
  • Interpretation:
    • Trafoschwingungen bei 50 Hz
    • Rauschen (Messfehler + allgemeine Störungen) als Untergrund
    • besondere Störung mit Grundfrequenz 39.6 Hz
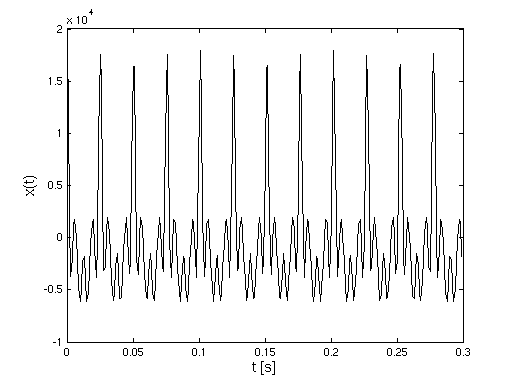
  • Analyse der Störung:
    • starke Impulse im Ortsraum
      
    • Unwucht in einer Welle, schlägt rhythmisch gegen das Lager
• Aufgaben:
  • Aufgabe 4
  • Aufgabe 5