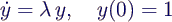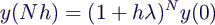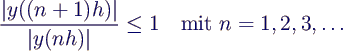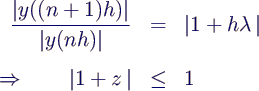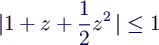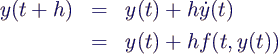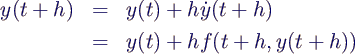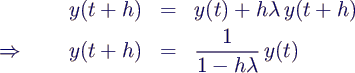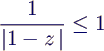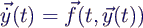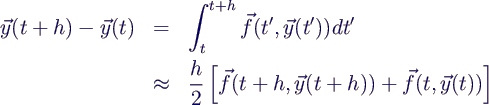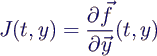Steife Probleme

• Steifer Tilger:
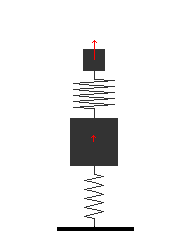
  • betrachtet wird wieder das System aus Schwinger und Tilger von oben
    • 
  • was geschieht, wenn die Feder zum Tilger immer steifer wird (d.h. ihre Federkonstante und Dämpfung nehmen stark zu)?
  • Erwartung
    • Tilger und Schwinger sind quasi "fest" miteinander verbunden
    • Schwinger bewegt sich wie ohne Tilger (bis auf dessen kleine Zusatzmasse)
    • Tilger bewegt sich in festem Abstand mit dem Schwinger mit
  • Ergebnis der Simulation für Faktor 100000
    • 
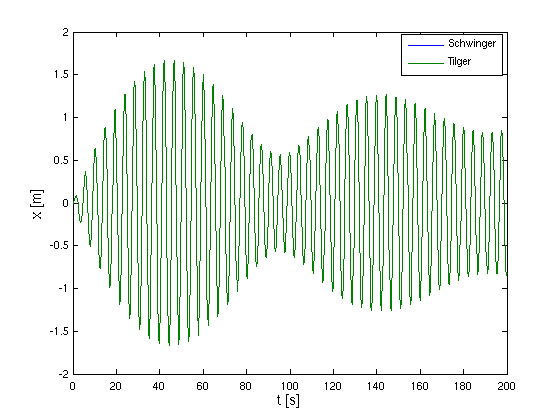
    • Schwinger und Tilger schwingen genau im Takt, minimaler Unterschied
    • 
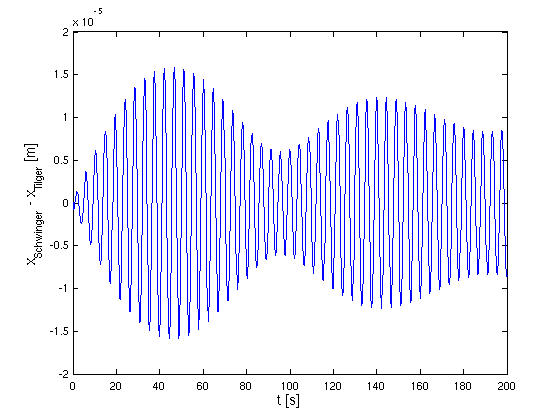
  • aber: Rechenzeit des Solvers (ode45) ist dramatisch angestiegen (Faktor 1000!)
• Schrittweiten beim Beispiel "Radioaktiver Zerfall":
  • System gegeben durch
    • 
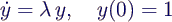
    • mit λ < 0
  • i. F. grundlegendes Beispiel
  • Simulation mit adaptivem Solver ode45 mit verschiedenen Genauigkeiten tol und für verschiedene Werte des Parameters λ
  • Zeitbereich jeweils von t = 0 bis t = 60
  • gemessen wird Zahl der Zeitschritte mit length(t)
  • Ergebnisse

    • tol	1e-3	1e-4	1e-5	1e-6
      -λ
      0.1	45	53	69	81
      10	773	793	809	817
      1000	72365	72381	72401	72409

  • 1. Beobachtung:
    • Zahl der Zeitschritte steigt nur langsam mit tol
    • Ursache: einfache glatte Lösungsfunktion exp(λ t)
  • 2. Beobachtung:
    • Zahl der Zeitschritte wächst stark für (betragsmäßig) großes λ
    • unverständlich, denn Lösung ist im Rahmen der geforderten Toleranz fast = 0!
  • typisches Verhalten "steifer" Systeme
• Untersuchung der Ursache beim Eulerverfahren:
  • Eulerverfahren liefert für N-ten Zeitschritt
    • 
  • für h λ < -1 wechselndes Vorzeichen
  • für h λ < -2 sogar betragsmäßig exponentieller Anstieg
  • also für großes negatives λ
    • Lösung ist völlig harmlos (i.w. = 0)
    • Verfahren funktioniert nur für sehr kleine Schrittweiten
  • ähnliches Verhalten bei allen bisher behandelten Verfahren
  • Grundproblem:
    • winzig kleine Störungen erzwingen winzige Schrittweiten
    • → lange Rechenzeiten
    • → ungenau wegen Aufschaukeln kleiner Fehler
• A-Stabilitätsgebiet eines Solvers:
  • Bereich für z = h λ (als komplexe Variable gedacht), in dem ein Verfahren für das Beispiel eine nicht-ansteigende Lösung liefert, d.h. es gilt
    • 
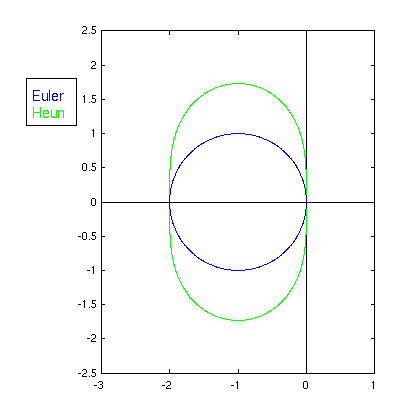
  • Beispiel Euler
    • 
  • Beispiel Heun
    • 
  • im Bild
    • 
• Implizites Eulerverfahren:
  • bei Euler: Ableitung am Startpunkt
    • 
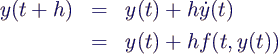
    • bei exponentiellem Abfall dort noch zu groß → Überschießen
  • statt dessen: Ableitung am Endpunkt
    • 
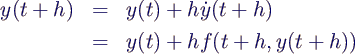
    • dort Ableitung schon klein → ok
  • Problem
    • gesuchte Größe y(t + h) auf beiden Seiten der Gleichung (nur implizit gegeben)
    • steht in Funktion f → Auflösung eines nichtlinearen Gleichungssystems nötig
    • iterativ, etwa mit Newton (mehrdimensional - i. a. sehr aufwändig!)
    • Vorteil: guter Startwert der Iteration vom letzten Zeitschritt
  • im Beispiel einfach explizit auflösen
    • 
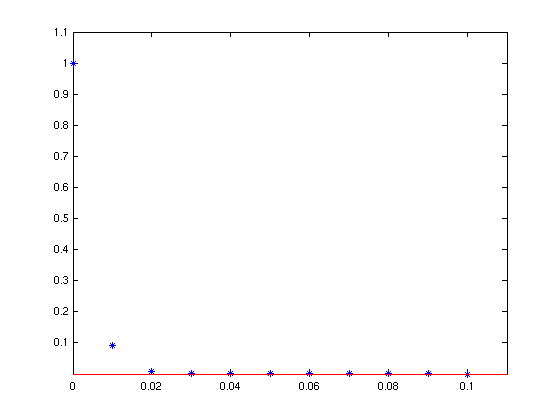
  • Ergebnis für λ = -1000 und Schrittweite 0.01
    • 
  • Stabilitätsgebiet
    • 
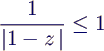
    • im Bild
    • 
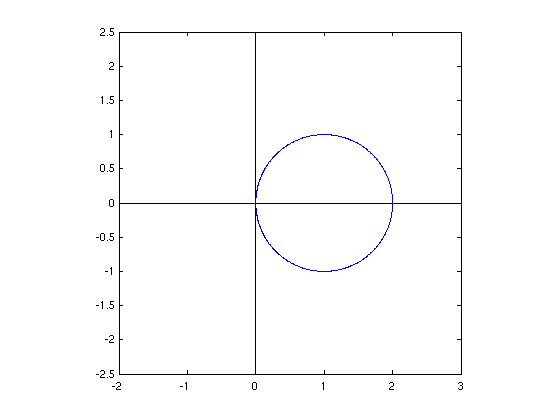
    • insbesondere für alle λ< 0 stabil
    • auch für viele λ > 0 stabil (unerwünscht!)
• Implizite Verfahren höherer Ordnung:
  • Trapez-Verfahren (2. Ordnung)
    • Integriere Differentialgleichung
    • 
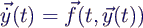
    • über [t, t+h] →
    • 
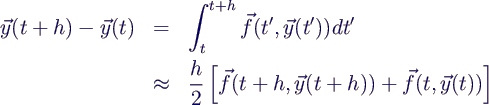
    • mit der Trapezregel
    • Stabilitätsgebiet: Im(z) < 0 (optimal)
  • weitere Verfahren als Runge-Kutta-Schema mit vollbesetzter Matrix B
  • Newton-Verfahren zur Lösung
    • braucht Jacobimatrix J der Differentialgleichung
    • 
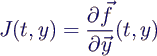
    • alternativ Ableitung numerisch nähern
• Beispiel van-der-Pool-Oszillator:
  • gegeben durch
    • 
  • als System
    • 
  • zugehörige Jacobimatrix
    • 
  • in Matlab
    • Funktionen f(t,y) und J(t,y) definieren
    • Jacobimatrix als Option bekanntmachen
    • options = odeset("Jacobian", J);
    • mit steifem Solver lösen, z.B. ode15s
• Aufgaben:
  • Aufgabe 21
  • Aufgabe 22