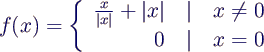Exercise 2: Continuity

• Exercise 2:
  • Study the continuity of the following real function on its maximal domain:
    • 
• Manual proof:
  • simplify f
  • prove continuity for x ≠ 0 with explicit ε-δ-approach
  • prove discontinuity for x = 0 again with ε-δ-approach
• Proving with Lean:
  • Mathlib defines continuity via open sets and filters
    • ContinuousAt f x
    • theorem continuousAt_iff provides usual ε-δ formulation
  • L2 delimits scope of local definitions
    • close with end LABEL or implicitely at end of file
  • L5 defines f
    • noncomputable, since construction of real numbers is non-computable
  • strategy
    • prove simplified formulae f_val_pos, f_val_neg for f (L10-36)
    • introduce auxiliary functions fp, fm for x > 0, x < 0 (L39f)
    • prove continuity of fp and fm (fp_is_cont, fm_is_cont) (L42-65)
    • show discontinuity of f at 0 (f_not_cont_at_0) (L70-97)
  • combine results
    • either use abstract lemmas (fp = f on open set, ...)
    • or prove continuity of f directly (L103ff)
• Lemmas f_val_pos, f_val_neg:
  • provide simplified expressions for f if x > 0 or x < 0
  • L11 defines x : ℝ with x > 0
  • L12-15 evaluation of if in definition as internal lemma
    • L14 if_pos replaces if-then-else by then branch and adds if-condition as assumption
    • L15 linarith combines linear relations or inequalities using hypotheses
  • L17 uses abs_of_pos: a > 0 → |a| = a
  • L7f trick to find this lemma
    • define relationship as simple example
    • apply? (hopefully) gives solution (often using exact)
  • remaining part with simple field and ring simplifiers
  • f_val_neg more cumbersome due to additional signs
    • L31-34 standard trick: prove auxiliary relation and use it with rw
• Lemma fp_is_cont:
  • fp continuous everywhere
  • proof closely follows usual procedure
  • L43f introduces x and definition of isContinuousAtX
  • L45 introduces ε > 0
  • L46 introduces working value ε for δ
    • goal is conjunction, includes δ > 0, i.e. ε > 0
  • L47 splits conjunction into two goals
  • L48 solves first goal (ε > 0) immediately
  • L49 introduces y with dist y x < ε
  • L50-52 insert definition of fp twice and solve the goal
• Lemma fm_is_cont:
  • lemma and proof for x < 0
    • basically identical
  • L63 small problem with proof
    • simp doesn't help due to additional signs
  • find lemma dist_neg_neg
    • either enter apply dist_ and scroll through the suggestions
    • or again with simple example and apply?
  • how to use it?
    • apply dist_neg_neg finds no dist (-a) (-b)
    • neither does rw [dist_neg_neg]
  • L63 rw [← dist_neg_neg] inserts an explicit minus
  • L64f simp and exact do the rest
• Lemma f_not_cont_at_0:
  • f discontinuous at 0
  • proof follows usual procedure
  • L72 push_neg handles the negation
  • L73-78 reduces goal to two simple inequalities
    • handle separately with · / ·
  • L79-82 proof first one
    • nice: simp replaces dist with |.|
  • L83-86 reduce the second one
    • uses dist_eq_abs (L67) to get rid of dist
  • L87-95 proof it by a simple calculation
    • calculations often are cumbersome!
• Wrapping up:
  • superficially we are ready
  • exact goal (L173) remains to be proven
    • ∀ x, isContinuousAtX f x ↔ x ≠ 0
    • needs continuity of f instead of fp/fm
    • could be done with some abstract nonsense
    • easier: explicitly
  • L103-114 y_between_x_0 as external lemma to use it for both cases
  • L116-139 replace fp_is_cont with direct proof for f
    • needs more care in choice of δ
    • L120 use min ε x
    • L126-130 show that y > 0 using y_between_x_0
  • L141-171 negative case, needs some extras, as always
  • L173-187 complete theorem
• Basic Lean skills:
  • how to work with quantifiers
    • ∀ x > 0 : intro x hx
    • ∃ x : use VAL
  • how to work with ∨ and ∧
    • ∧ in goal: constructor
    • ∨ in hyp: rcases
  • how to find lemmas in Mathlib
    • formulate examples
    • apply?, exact?, rw?
    • scroll through suggestions
    • visit Mathlib files via definitions
  • how to prove simple relations
    • formulate parts as hypotheses
    • use explicit calculations with calc