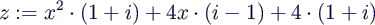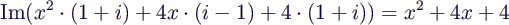Exercise 1: Complex numbers

• Exercise 1:
  • For which values of x ∈ ℝ is
    • 
  • real?
• Manual proof:
  • reformulation
    • For which values of x ∈ ℝ is Im(z) = 0?
  • compute
    • 
  • solve quadratic equation to get
    • x = -2
• Using examples:
  • lemmas without name
  • good place to try some simpler steps by itself
  • Lean shows tactic state after each step
    • contains all (proven) assumptions
    • shows remaining goal
  • L4f simple algebraic manipulation
    • solved by tactic ring
    • uses axioms and simple lemmas of commutative rings
    • tries to prove equations or inequalities
  • alternatives
    • ring_nf tries to bring expression into "normal form"
    • simp tries many "simplifying" lemmas
• Proof in Lean:
  • L16f formulation of the lemma
  • L18 Formulate step 2 as new hypothesis
    • L19 simp reduces to
    • (↑x ^ 2).re + (↑x ^ 2).im = x ^2
  • seems to be trivial, what is the problem?
  • L10f try as example
    • (x : ℝ) : (x^2).im = 0
    • → error, no Real.im
  • L13 cast x to complex
    • simp doesn't work, problem with changing type of x
    • tactic norm_cast for such cases → works (L14)
  • back to h1
    • L20 norm_cast proceeds to
    • x ^ 2 + 0 = x ^ 2
    • L21 ring finishes proof of h1
  • L22 uses h1 with
    • rw [h1]
    • leads to
    • x^2 + 4*x + 4 = 0 ↔ x = -2
  • using manual result of step 3 to rewrite polynom
    • L23 formulation as h2
    • x ^ 2 + 4 * x + 4 = (x + 2)^2
    • ring proves immediately
  • L25 using h2 leads to
    • (x + 2) ^ 2 = 0 ↔ x = -2
    • simp gets rid of square
    • x + 2 = 0 ↔ x = -2
  • trivial, there should be a simple algebra theorem for that
    • apply? finds the theorem in Mathlib.Algebra.Group.Basic
    • eq_neg_iff_add_eq_zero : a = -b ↔ a + b = 0
    • Iff.symm uses symmetry of ↔
    • L27 exact finishes the proof
• Basic Lean skills:
  • exact formulation of task
  • simple calculations with rw
  • employing basic lemmas