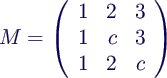Exercise 3: Matrix Rank

• Exercise 3:
  • Given c ∈ ℝ and the matrix
    • 
  • Compute rank(M) for all values of c.
• Manual proof:
  1. compute
     • det(M) = (c - 3)*(c - 2)
  2. using Cramer's rule for the determinant of a 3x3 matrix
  2. use theorem 1
     • A nxn: rank(M) = n ↔ det(M) ≠ 0
  3. to get
     • (c ≠ 2 ∧ c ≠ 3) ↔ M.rank = 3
  3. for c = 2, 3 give explicit submatrices S2, S3 with rank 2
  4. use theorem 2
     • B submatrix of A → rank(B) ≤ rank(A)
  5. together with 2. one gets
     • (c = 2 ∨ c = 3) → rank(M) = 2
• Linear Algebra in Mathlib:
  • mostly for modules (i.e. over a ring, not a field)
    • → some important theorems are not true in this generality
  • property isUnit
    • means: ring element is invertible
    • used for det as well, since generally K is a ring
    • here K is a field → (isUnit a ↔ a ≠ 0)
  • definition of a matrix
    • Matrix m n R
    • entries from ring R
    • m, n index types
    • very often m = (Fin k) = {0, 1, .., (k-1)} with k : ℕ
  • definition of a submatrix
    • submatrix M f e
    • with matrix M m n R
    • and reindexing functions f : m₀ → m, e : n₀ → n
• Providing theorems 1 & 2:
  • L11-51 proof of theorem 1 (max_rank_iff_det_ne_zero)
    • needs some abstract nonsense
  • L53-72 proof of theorem 2 (rank_submatrix_le)
    • slight extension of theorem from Mathlib
    • has now been included in Mathlib
• Proving with Lean:
  • follows closely the manual proof
  • step 1 = lemma det_M
  • step 2 = lemma rank3_M
    • det_M_eq_zero analyzes the explicit form of the determinant
    • rank3_M applies theorem 1
  • step 3 = lemma rank2_M
    • define matrix Sc (c=2,3) (L106f)
    • show that Sc is submatrix of M (lemma Sc_is_submatrix)
    • show that rank Sc = 2 (lemma Sc_rank_2)
    • use theorem 2 to show M.rank ≥ 2 (lemma rank_ge_2_M)
    • use rank3_M to conclude M.rank = 2 (lemma rank2_M)
• Remarks:
  • L85f write Cramer's rule explicitely → apply? finds det_fin_three
  • L96ff tricky to avoid clumsy constructor/intro/rcases
    • Iff.symm converts a ↔ b into b ↔ a
  • L110-112 define functions to extract rows (f2/3) and columns (e)
  • L121f idea: compute det(Sc * Scᵀ)
  • L123f: necessary, since simp can't compute the transpose of a matrix
  • L164-169 adapt hypotheses to det_M_eq_zero
    • tauto helps with general logic stuff
  • L170ff trivial but cumbersome, idea:
    • rank ≤ 3 (sure, M is 3x3)
    • rank ≠ 3 (since det M = 0)
    • → rank ≤ 2 (rank is in ℕ)
    • rank ≥ 2 (rank_ge_2_M)
    • that should do it!
• Basic Lean skills:
  • working with Mathlib
  • tearing and combining of lemmas
  • adapting hypotheses