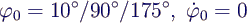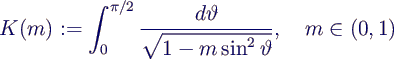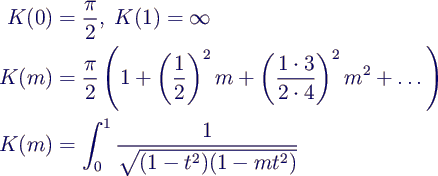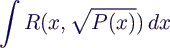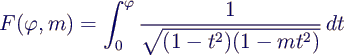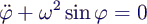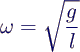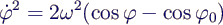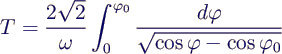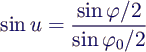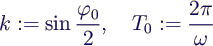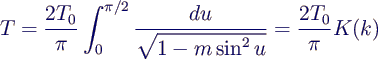Definite Integrals

• Exercise 3:
  • given a mathematical pendulum of length l = 1 m
  • compute oscillation period for initial values
    • 
  • mathematical problem: compute a complicated integral
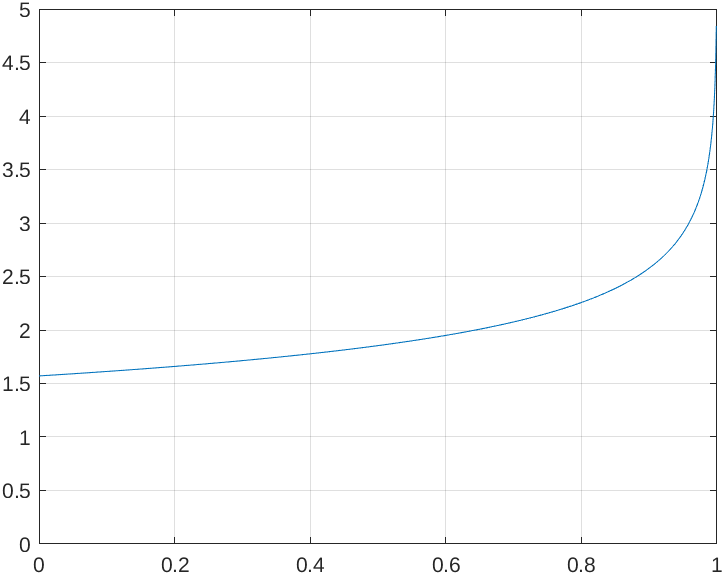
• Special function:
  • complete elliptic integral of the first kind K
    • 
    • 
  • important properties
    • 
  • computation in Matlab
    • directly defined as ellipke(m)
• Related functions:
  • elliptic integrals
    • 
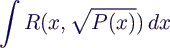
    • P(x) polynomial of degree 3 or 4
    • R rational function of its two arguments
  • important special case: incomplete elliptic integral of the first kind
    • 
  • inverse of F (Jacobi elliptic functions)
• Further applications:
  • in mathematics
    • geometry (e. g. arc length of ellipse)
    • complex functions (doubly periodic functions)
    • very important further developments (elliptic curves, modular forms, Fermat, ...)
    • solution of quintic equations
  • trajectory of the mathematical pendulum
  • form of a skipping rope
  • soliton waves
  • cryptography (ok, needs some steps from here ...)
• Solution of exercise 3:
  • equation of motion
    • 
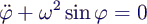
    • with
    • 
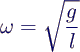
  • energy conservation →
    • 
  • integration from 0 to T/4 →
    • 
  • substitution
    • 
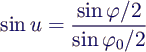
    • and abbreviations
    • 
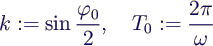
    • result in
    • 
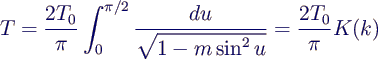
  • numerically

    • φ0	T	|T - T0|/T0
      10°	2.0521	0.0229
      90°	2.6640	0.3280
      175°	6.2141	2.0977