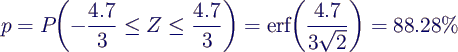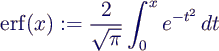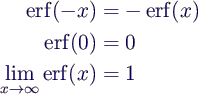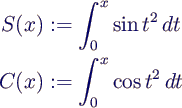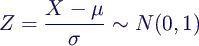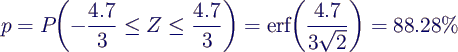Antiderivatives

• Exercise 2:
  • manufacturing process for electrical resistors with R = 47 kΩ
  • actual values normally distributed with E(X) = 47 kΩ, σ(X) = 3 kΩ
  • using norm series E12 → R may differ by 10% from denoted value
  • compute percentage of produced resistors in the allowed range
  • mathematical problem: compute antiderivative of exp(-x²)
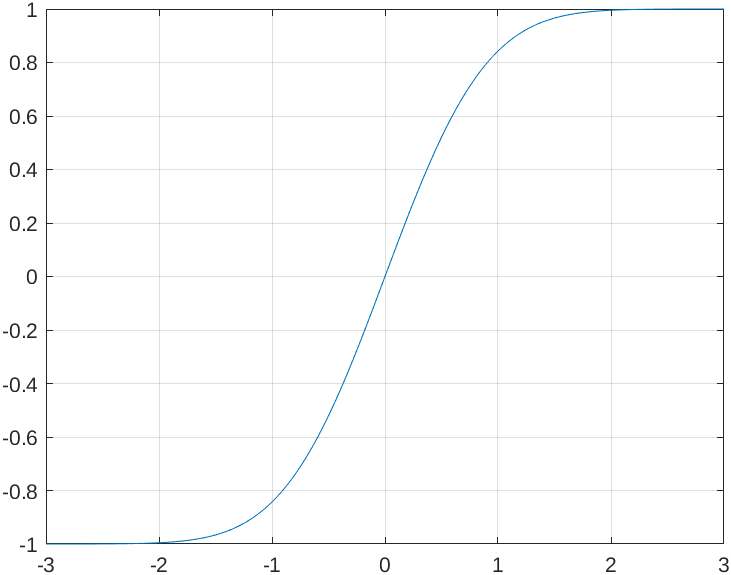
• Special function:
  • error function
    • 
    • 
  • important properties
    • 
  • computation in Matlab
    • directly defined as erf(x)
    • useful for large x: erfc(x) = 1 - erf(x)
• Related functions:
  • Fresnel integrals
    • 
• Further applications:
  • everywhere in statistics
    • very common distribution function due to central limit theorem
  • variant: Maxwell distribution of molecule velocities in an ideal gas
  • solution of the heat equation
  • Fresnel integrals
    • scattering of light around obstacles
    • motorway exits
• Solution of exercise 2:
  • distribution of resistance values
    • X ~ N(47, 9)
  • compute p as
    • p = P(0.9*47 ≤ X ≤ 1.1*47)
  • normalizing
    • 
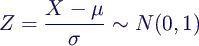
    • leads to
    •