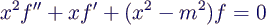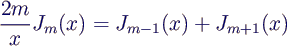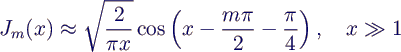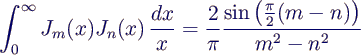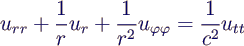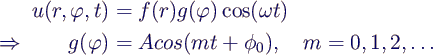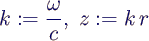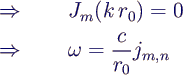Differential Equations

• Exercise 4:
  • given a circular membrane with wave speed c fixed at radius r₀
    • c can be computed from membrane properties like elasticity and density
  • compute the frequencies of the first 10 vibration modes
  • mathematical problem: solve a differential equation
• Special function:
  • Bessel functions J_m, Y_m, m = 0, 1, 2, ...
    • solutions of the Bessel equation
    • 
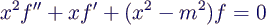
    • J_m finite at x = 0
    • Y_m has pole at x = 0
    • 
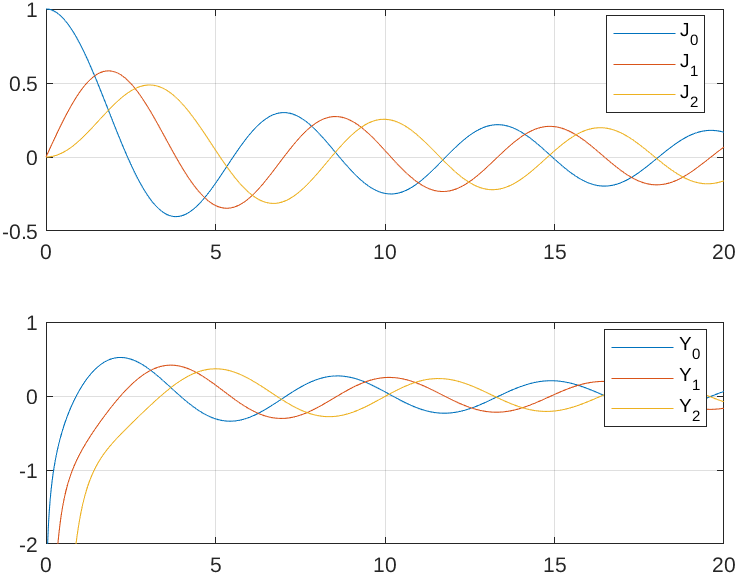
    • zeros at j_m,n, y_m,n for n = 1, 2, ...
  • important properties
    • recurrence relation
    • 
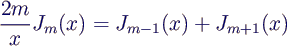
    • asymptotic behaviour for large x
    • 
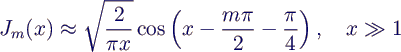
    • orthogonality
    • 
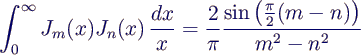
  • computation in Matlab
    • directly defined as besselj(m,x), bessely(m,x)
    • helpful function besselzero for computation of zeros available
• Related functions:
  • Hankel functions
    • complex linear combinations of J_m, Y_m
  • spherical Bessel functions
    • halbzahliges m
• Further applications:
  • all kinds of phenomena with cylindrical symmetry, e. g.
    • electromagnetic waves in a waveguide
    • heat conduction
    • eigen vibrations of a circular plate
  • diffraction through an aperture
  • electric filters
• Solution of exercise 4:
  • 2-d wave equation in polar coordinates
    • 
  • eigen modes and separation of variables
    • 
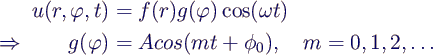
    • with
    • 
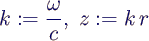
    • → Bessel equation for f(z)
    • continuous at r = 0 → only J_m
  • fixed at circle r = r₀
    • 
  • table of j_m,n gives lowest modes and frequencies

    • n m	1	2	3	4
      0	2.40	5.52	8.65	11.79
      1	3.83	7.02	10.17	13.32
      2	5.14	8.42	11.62	14.80
      3	6.38	9.76	13.02	16.22
      4	7.59	11.06	14.37	17.62
      5	8.77	12.34	15.70	18.98