Wärmeaufnahme eines Kühlrohrs
- Problemstellung:
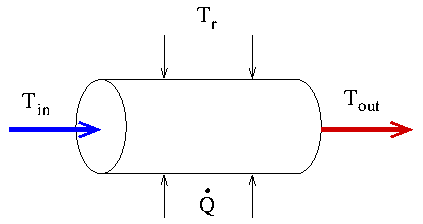
- in ein Kühlrohr wird Fluid (Flüssigkeit oder
Gas) der Temperatur Tin gepumpt
- das Rohr nimmt die
Wärmemenge
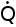 aus der heißen Umgebung (Temperatur Tr) auf
aus der heißen Umgebung (Temperatur Tr) auf
- dadurch erwärmt sich das Fluid auf Tout
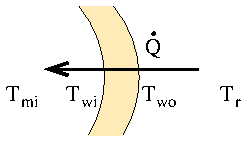
- Wärme durchläuft dabei mehrere Schichten
- Wärmedurchgang vom Raum zur äußeren Rohrwand
(Tr → Two)
- Wärmeleitung durch die Rohrwand (Two
→ Twi)
- konvektiver Übergang von der Rohrwand zur
Flüssigkeit (Twi → Tmi :=
(Tin + Tout)/2)
- gesucht:
Wärmemenge
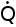 , Temperaturen Two, Twi,
Tout
, Temperaturen Two, Twi,
Tout
- Bilanzgleichungen:
- Vereinfachung: Twi, Two längs
Rohr konstant
- damit
- alle Stoffgrößen und Übergangskoeffizienten
αi hängen in komplizierter Weise von den
Ti ab
- 4 Gleichungen für 4 Unbekannte mit folgender Struktur
- System kann in verschiedener Weise auf eine Gleichung
reduziert werden
- Lösung mit Nullstellensuche:
- Grundschema mit Basisvariable Tout
- (G1) nach
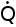 auflösen →
auflösen →
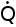 (Tout) (analytisch)
(Tout) (analytisch)
- (G2) mit (a) nach Twi auflösen
→ Twi(Tout) (numerisch)
- (G3) mit (a), (b) nach Two auflösen
→ Two(Tout) (numerisch)
- (G4) mit (a), (c) → Gleichung für
Tout (numerisch)
- sichere Intervalle für fzero
- Twi ∈ [Tin,
∞)
- Two ∈ [Twi,
∞)
- Tout ∈ [Tin,
Tmax] mit
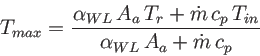
- Beweise
- physikalisch leicht herleitbar
- mathematisch unter Annahmen an die
Stoffbeziehungen
- in allen untersuchten Beispielen (Gase +
Flüssigkeiten) erfüllt
- fzero mit Intervall [T0, ∞)
- wähle obere Grenze T1
- kein Vorzeichenwechsel → verdoppele
Intervallbreite (bei festem T0)
- Lösung mit Fixpunkt-Iteration:
- Idee stammt aus Praxisprojekt
- Vorgehen ähnlich wie oben
- Problem mit (d): Tout kommt in (G4)
nicht vor
- Grundschema
- wähle Startwert für Tout
- aus (G1)
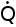 bestimmen (analytisch)
bestimmen (analytisch)
- aus (G2) mit (b) Twi bestimmen
(numerisch)
- aus (G3) mit (b), (c) Two bestimmen
(numerisch)
- aus (G4) mit (d)
neues
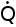 bestimmen (analytisch)
bestimmen (analytisch)
- aus (G1) mit (e) neues Tout
bestimmen (numerisch)
- drei numerische Teilschritte (c), (d), (f)
- mit Sub-Iterationen
- in folgender Analyse der Einfachheit halber direkt
mit fzero
- guter Startwert Tout,0 = (Tin +
Tmax)/2 von oben
- numerische Ergebnisse
- konvergiert bei vielen Parametersätzen und
Materialien
- divergiert z.B. bei Wasser/Frigen
- in der Literatur komplexe Subiterationen für ähnliche
Probleme
- Fazit: Konvergenz nur bei bestimmten Stoffen
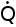 aus der heißen Umgebung (Temperatur Tr) auf
aus der heißen Umgebung (Temperatur Tr) auf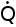 , Temperaturen Two, Twi,
Tout
, Temperaturen Two, Twi,
Tout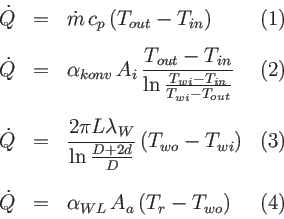
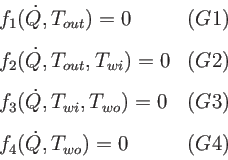
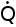 auflösen →
auflösen →
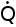 (Tout) (analytisch)
(Tout) (analytisch)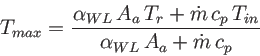
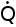 bestimmen (analytisch)
bestimmen (analytisch)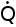 bestimmen (analytisch)
bestimmen (analytisch)
