Problemstellung:
- Finde approximative Lösung der Poisson-Gleichung
auf einem rechteckigen Gebiet für gegebene Quellen f und Randwerte u.
Diskretisierung:
- Kontinuum ersetzt durch Gitter, Ableitung durch Differenzenquotient
- Am Rand u-Werte durch vorgegebene Randwerte ersetzen.
Umschreiben auf lineares Gleichungssystem:
- Umbau von 2d-Gitter auf 1d-Index:
- Aus diskretisierter Poisson-Gln. wird:
- Auftretende Randwerte auf die rechte Seite, i.f. = 0.
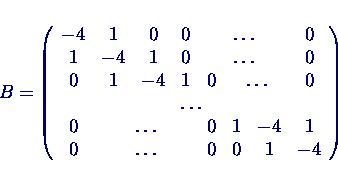
- Damit schreibbar als
wobei
I = nxn-Einheitsmatrix
Sourcen:
Lösung des Gleichungssystems:
- A:
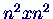 - Matrix
- Matrix
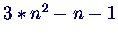 Elemente
Elemente 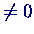
- rechte Seite: Punkt-Quadrupol
- verwende Sparse Solver von Veclib
- Speicherbedarf von A bei n = 500:
| full: |
500 000 MB |
| sparse: |
6 MB |
| zur Lösung: |
300 MB |
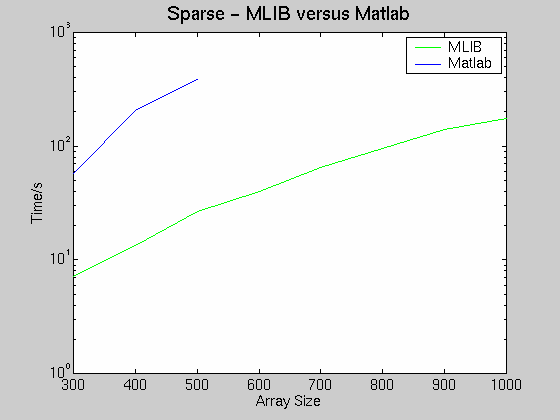
Performance-Messungen:
- skalar:
- parallel:
- MLIB-Manual: dsleda ist parallelisiert
- keine Beschleunigung bei mehr CPUs!
- Analyse mit CXperf:
- 30% Zeitanteil für dslefa
- CPU/Wall = 1.0 für dslefa (und alle anderen Routinen)
 ist nicht parallel!
ist nicht parallel!




Peter Junglas 20.6.2000
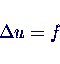
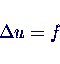
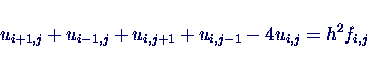
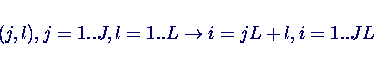
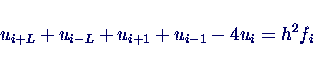
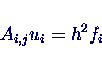

![]()