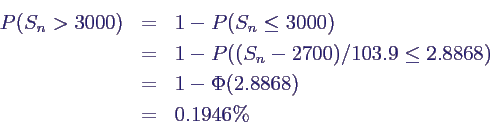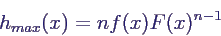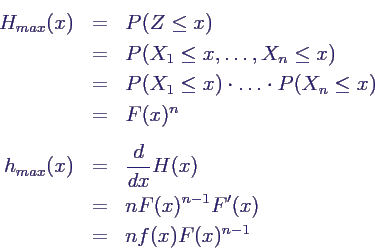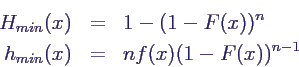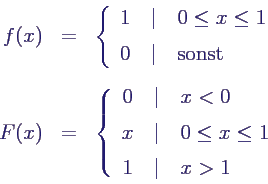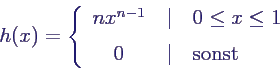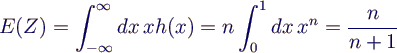Unabhängige Zufallsvariablen
- Unabhängigkeit mehrerer Zufallsvariablen X1,
.., Xn:
- Wahrscheinlichkeits- bzw. Dichtefunktion faktorisiert
- p(x1, ..., xn) = p(x1)
... p(xn) (diskret)
- f(x1, ..., xn) = f(x1)
... f(xn) (stetig)
- vereinfacht Berechnungen erheblich
- X, Y unabhängig ⇒
- E(X Y) = E(X) E(Y)
- Var(X + Y) = Var(X) + Var(Y)
- weitere Vereinfachung: alle Xi haben
gleiche Verteilung
- Bezeichnung: i.i.d. = independent identically
distributed
- häufig gute Annahme für Messreihen
- Beispiel Rundungsfehler:
- Zahlenwerte im Computer
- sind auf feste (binäre) Stellenzahl gerundet
- Rechenergebnisse haben Rundungsfehler
- Standardgenauigkeit δ ≈ 2 · 10-16
- Abweichung maximal δ/2
- Annahmen (meistens gut erfüllt)
- Rundungsfehler X gleichverteilt im Intervall
[-δ/2, δ/2]
- Rundungsfehler von Teilrechnungen unabhängig
voneinander
- für Einzelfehler
- Zufallsvariable S für Summe aus n
Größen
- mittlerer Fehler wächst mit
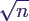 , nicht mit n
, nicht mit n
- Grund: positive und negative Fehler heben sich
teilweise auf
- Summe unabhängiger Zufallsgrößen:
- X, Y unabhängige Zufallsvariable mit Dichten
f(x), g(y)
- gesucht: Dichtefunktion h(z) von Z = X + Y
- Ergebnis
- Beweis
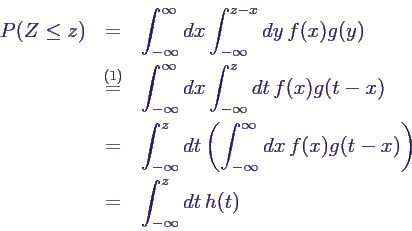
- mit der Substitution t = x + y, dt = dy bei (1)
- Spezialfälle
- Beispiel Beladung eines Schmelzofens:
- Schmelzofen wird mit Kisten aus Ausschussmaterial
beladen
- Behälter für Schmelze fasst maximal
3000 kg
- unterschiedliche Masse pro Kiste, Verteilung X ~
N(100 kg, 400 kg2)
- wird mit n = 27 Kisten beladen
- Gesamtladung Sn des Ofens also
normalverteilt mit
- E(Sn) = n E(X) = 2700 kg
- Var(Sn) = n Var(X) = 10800 kg2
- σ(Sn) = 103.9 kg
- Wahrscheinlichkeit für Überladung
- Maximum und Minimum unabhängiger
Zufallsgrößen:
- gegeben: n i.i.d. Zufallsvariablen Xi mit
Dichte f(x) und Verteilungsfunktion F(x)
- gesucht: Dichte hmax(z) von Z = Max(Xi)
- Ergebnis
- Beweis
- analog für das Minimum
- Beispiel Gleichverteilung:
- n in [0,1] gleichverteilte Zufallszahlen Xi
- gesucht: Erwartungswert für Maximalwert Z
- Dichte und Verteilungsfunktion der einzelnen Xi
- mit obigen Formeln
- Erwartungswert
- z. B. für n = 10
- E(Z) = 10/11 = 0.9091
- P(Z ≤ 0.9) = 0.910 = 34.87 %
- Aufgaben:



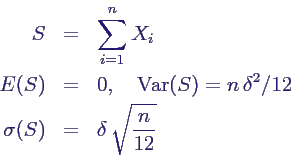
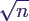 , nicht mit n
, nicht mit n