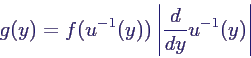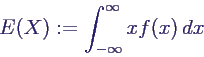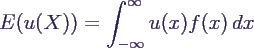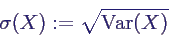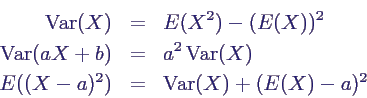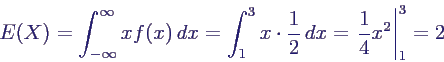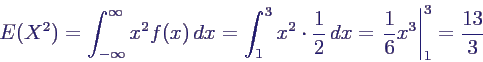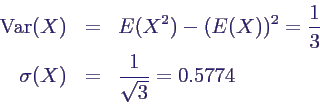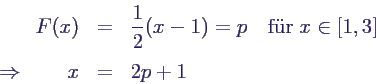Eigenschaften stetiger Verteilungen

• Transformations-Formel:
  • gesucht sei Wahrscheinlichkeitsdichte von Funktion von X, etwa X², log(X)
  • allgemein Y = u(X) mit u streng monoton
  • Satz: Y hat die Dichte
    • 
  • Beweisidee: berechne Verteilungsfunktion von Y und verwende Substitution
  • Beispiel: X habe nur positive Werte, gesucht Dichte von X²
    • 
• Erwartungswert einer stetigen Zufallsvariablen:
  • X sei stetige Zufallsvariable mit Wahrscheinlichkeitsdichte f
    •  Erwartungswert E(X) (oder μ_X)
    • 
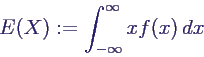
  • Eigenschaften wie im diskreten Fall
    • E(aX) = a E(X)
    • E(X + Y) = E(X) + E(Y)
    • E(1) = 1
  • außerdem gilt
    • 
• Varianz und Standardabweichung:
  • definiert wie im diskreten Fall
    • Var(X) := E((X - E(X))²)
    • 
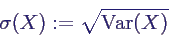
  • Eigenschaften wie oben
    • 
• Median und Quantile:
  • X stetige Zufallsvariable → Verteilungsfunktion macht keine Sprünge
  • Für p ∈ [0,1] ist das p-Quantil von X ein Wert x_p mit
    • F(x_p) = p
  • Das 0.5-Quantil heißt wieder Median.
  • F streng monoton → Quantile eindeutig bestimmt
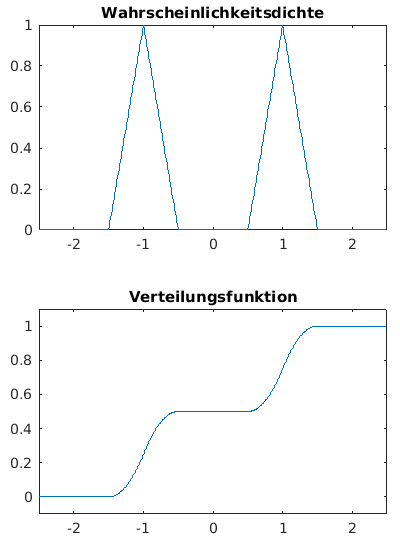
  • Beispiel für nicht-eindeutigen Median
    • Dichtefunktion mit zwei Maxima (bimodal) und Nullbereich
    • 
• Beispiel Gleichverteilung:
  • Beispiel von oben (Gleichverteilung im Intervall [1,3])
  • Berechnung des Erwartungswerts
    • 
  • Berechnung der Varianz
    • 
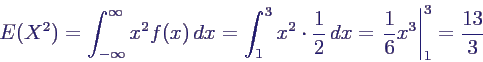
    • daher
    • 
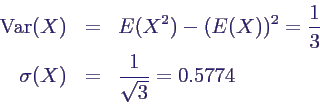
  • Berechnung von Median, 5%- und 95%-Quantilen
    • 
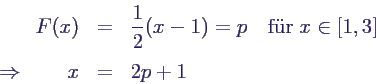
    • also
    • x_0.5 = 2
    • x_0.05 = 1.1
    • x_0.95 = 2.9
• Aufgaben:
  • Aufgabe 11