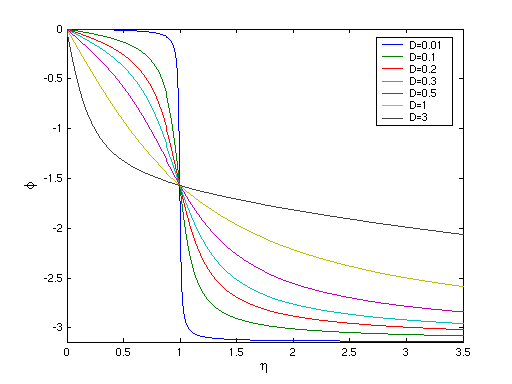
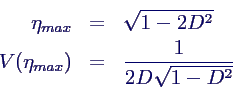Harmonische Anregung

• Simulation:
  • 
  • Verhalten bei b/m = 0.3/s, c/m = 1/s² und verschiedenen Anregungsfrequenzen
  • Ω = 0.5/s
    • erst Einschwingen, dann harmonische Schwingung
    • folgt Anregung leicht phasenverschoben
  • Ω = 1.0/s
    • sehr große Amplitude (Resonanz) um π/2
    • zur Anregung phasenverschoben
  • Ω = 2.0/s
    • wieder kleinere Amplitude
    • Phasenverschiebung fast π (gegenläufig zur Anregung)
• Lösung der Bewegungsgleichung:
  • Erregerfunktion ist harmonische Schwingung
    • 
  • allgemeine Lösung besteht aus Überlagerung zweier Schwingungen
    • x(t) = x_homogen(t) + x_part(t)
  • x_homogen(t)
    • Lösung der Gleichung ohne Anregung (homogene Gleichung)
    • gedämpfte Schwingung oder (für D > 1) Kriechen
    • enthält Abhängigkeit von Anfangsbedingungen
    • meistens irrelevant
    • nötig, wenn Maximalamplitude gesucht
• Bestimmung einer partikulären Lösung:
  • am einfachsten im Komplexen als Realteil der Lösung von
    • 
  • Lösungsansatz: Schwingung mit Anregungsfrequenz
    • 
  • Einsetzen ergibt
    • 
    • 
  • durch Zerlegen von H in Polarform
    • 
  • erhält man
    • 
  • Lösung damit
    • 
  • Vergrößerungsfunktion V = Vielfaches der Amplitude im Vergleich mit statischer Anregung
    
  • Einführen des Frequenzverhältnisses
    • 
  • liefert
    • 
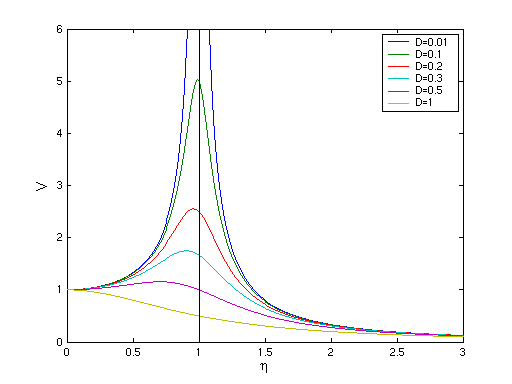
• Vergrößerungsfunktion:
  • graphisch
    
  • für kleine Dämpfung (D << 1): Maximum bei η = 1 (Resonanz)
  • Maximalwert für D < 1/:
    • 
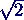• Phasenwinkel:
  • graphisch
    
  • besondere Fälle:
    • niedrige Anregungsfrequenz → Masse folgt direkt
    • Resonanz → Phasenverschiebung = π/2
    • hohe Anregungsfrequenz → gegenläufige Bewegung
• Aufgaben:
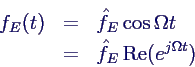
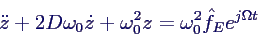
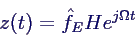
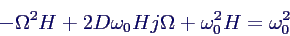
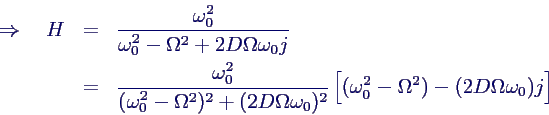
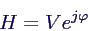
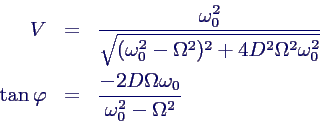
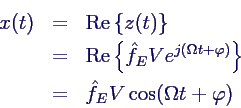
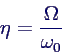
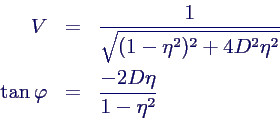
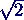  • Aufgabe 19
  • Aufgabe 20
  • Aufgabe 21