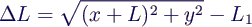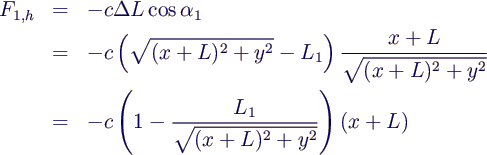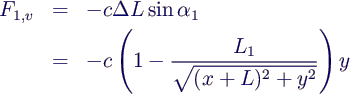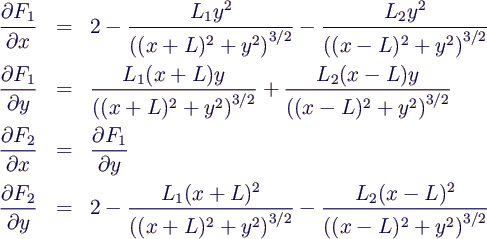Lösung von Aufgabe 8

• Kräftebilanz:
  • An der Position (x, y) beträgt die Auslenkung der 1. Feder
    • 
  • die Rückstellkraft ist also in horizontaler Richtung
    • 
  • in vertikaler Richtung
    • 
  • Berücksichtigt man analoge Beziehungen für die 2. Feder sowie die Gewichtskraft der Masse, erhält man sofort das angegebene System für die Kräftebilanz in horizontaler und vertikaler Richtung.
• Bestimmen der Lösung mit dem Newton-Verfahren:
  • Zunächst muss die Jacobi-Matrix berechnet werden. Nach sorgfältiger Rechnung (und leichten Zusammenfassungen) erhält man
    • 
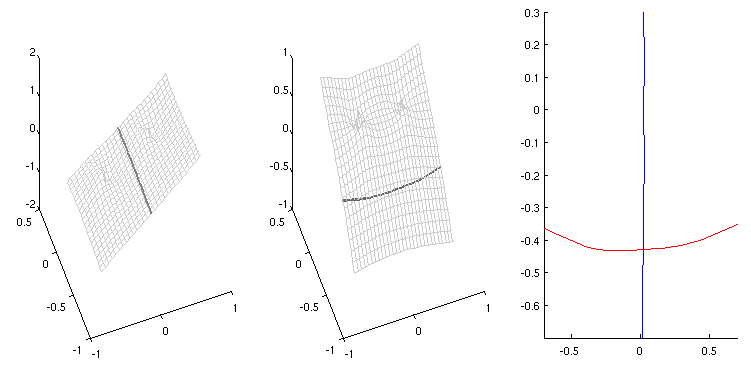
  • Mit plotZeros verschafft man sich zunächst einen Überblick
    • 
  • und liest als Startwert ab:
    • x0 = [0; -0.4]
  • Mit Hilfe der Funktion solveNewton aus der Vorlesung erhält man sofort die Lösung
    • x = [0.0201; -0.4292]
  • Alle Berechnungen können mit dem Matlab-Skript ex08b.m ausgeführt werden.
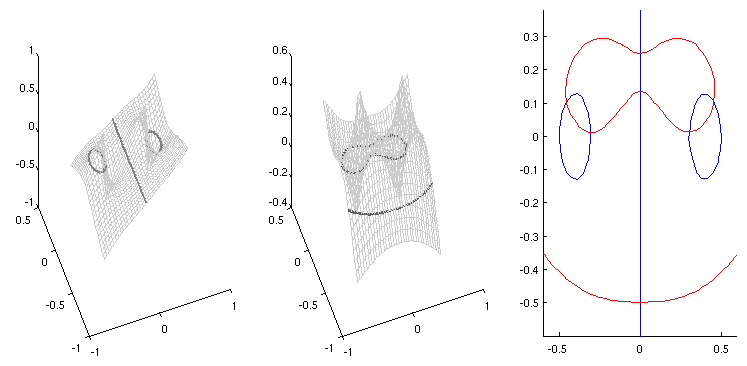
• Lösungen bei hoher Vorspannung:
  • Mit den neuen Werten erhält man als Plot
    • 
  • Man erkennt 3 Schnittpunkte auf der Symmetrieachse und je zwei Punkte auf der linken und rechten Seite, aufgrund der Symmetrie (L₁ = L₂) spiegelbildlich angeordnet.
  • Ablesen der Startwerte (unter Zuhilfenahme der Lupe des Matlab-Plots) liefert auf der y-Achse die Ergebnisse
    • y1 = -0.4985, y2 = 0.1346, y3 = 0.2501
  • Mit dem Startwert
    • x04 = [0.45; 0.10]
  • bekommt man auch den oberen der seitlichen Punkte bei
    • x = [0.4543; 0.1050]
  • Der untere Punkt (etwa bei [0.3; 0.02]) wiedersetzt sich hartnäckig: Das Newton-Verfahren konvergiert regelmäßig gegen einen der anderen Werte, wie dicht man auch versucht, an den Wert zu kommen (etwa durch höher aufgelöste Plots). Geht man zurück in die Formel für die Kräfte, wird die Ursache klar: Die Position liegt genau auf dem Fußpunkt der 2. Feder, sie hat dann die Länge 0. Dadurch wird der Richtungsvektor undefiniert, die Funktion liefert in Matlab den Wert NaN.
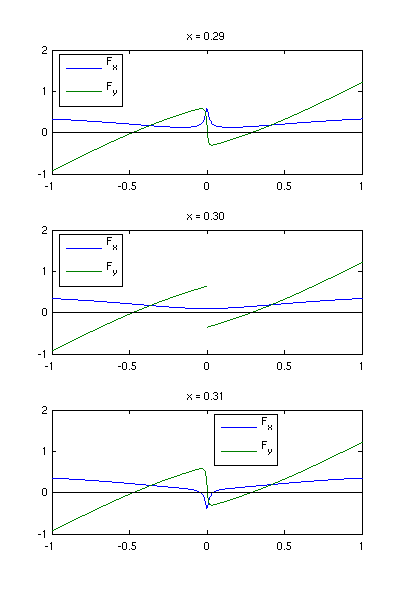
  • Um zu verstehen, wieso im Plot falsche Nullstellen auftreten, untersuchen wir die kritische Stelle (0.3, 0.0) genauer und plotten drei Kurven für F_x und F_y, jeweils für x = 0.29, 0.30 und 0.31, und variables y:
    • 
    Die y-Komponente der Kraft ist hier unstetig!
  • Physikalisch ist klar, dass hier keine Gleichgewichtsposition zu finden ist: Die Federn liegen horizontal, sie können die vertikale Gewichtskraft nicht ausgleichen. Abgesehen davon: Mit der Länge 0 hat man sicher den Linearitätsbereich jeder realen Feder verlassen!
  • Alle Rechnungen können mit ex08c.m nachvollzogen werden.