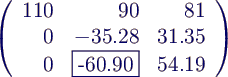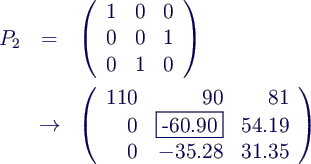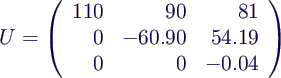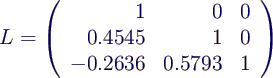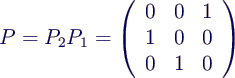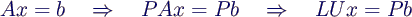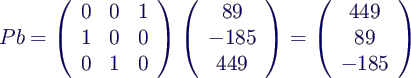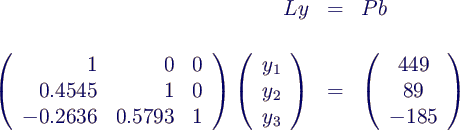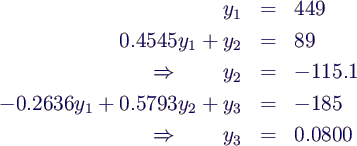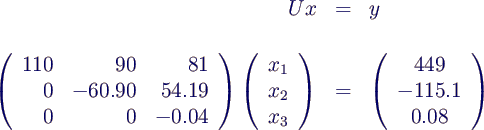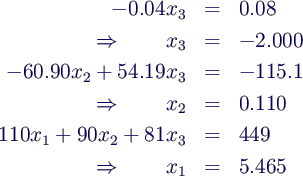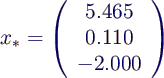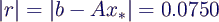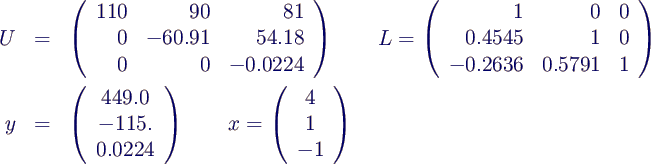Lösung von Aufgabe 3

• Alle Berechnungen können mit dem Matlab-Skript ex03.m ausgeführt werden. Das Runden kann sehr einfach erledigt werden mit round(x, 4, "significant"), allerdings wird dabei bei 0.5 immer aufgerundet. Die kleine Hilfsfunktion runde.m implementiert dagegen "round-to-even" und liefert, obwohl der Unterschied nur zweimal zum Tragen kommt, deutlich andere Werte für x.
  
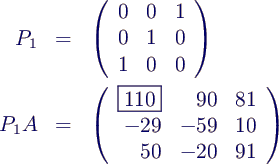
  • LU-Zerlegung von A:
    1. Vertauschung von 1. und 3. Zeile
       • 
    2. 1. Zeile mit q₁ = -29/110 ≈ -0.2636 multiplizieren und von der 2. Zeile subtrahieren. 1. Zeile mit q₂ = 50/110 ≈ 0.4545 multiplizieren und von der 3. Zeile subtrahieren
       • 
    3. Vertauschung von 2. und 3. Zeile
       • 
    4. 2. Zeile mit q₃ = 35.28/60.90 ≈ 0.5793 multiplizieren und von der 3. Zeile subtrahieren
       • 
    5. L aus den q's zusammensetzen, dabei Vertauschung in Schritt 3 berücksichtigen
       • 
    6. gesamte Permutationsmatrix als Produkt der Teilpermutationen
       • 
       Reihenfolge klar, da immer von links an A heranmultipliziert wird
    7. Kontrolle der Zerlegung
       • 
  • Lösung von A x = b:
    • Berücksichtigung von P
      • 
    • also Vorwärts-/Rückwärtssubstitution für rechte Seite
      • 
    • Vorwärtssubstitution
      • 
    • ergibt (bei Rundung in jedem Rechenschritt!)
      • 
    • Rückwärtssubstitution
      • 
    • man erhält
      • 
    • Ergebnis der Rechnung also
      • 
    • Residuum
      • 
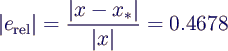
    • relativer Fehler
      • 
  • Lösung mit Matlab:
  • Mit
    • [L, U, P] = lu(A)
      y = L \ (P*b)
      xSc = U \ y
  • erhält man wesentlich genauere Werte für L, U, y und x
    • 
  • Die kleinen Unterschiede in den letzten Zeilen zeigen, wie sich die Rechenfehler bei Rundung hier aufschaukeln.
  • Residuum und relativen Fehler bestimmt man mit
    • rC = norm(A*xSc - b)
    • eC = norm(x - xSc)/norm(x)
  • zu
    • rC = 2.8422 · 10^-14
    • eC = 4.4758 · 10^-13
  • Die rechte Seite der Ungleichung bestimmt man (für Teil c. bzw. b.) leicht zu
    • rhsC = 1.1914· 10^-12
  • bzw.
    • rhsB = 3.1510
  • in beiden Fällen deutlich größer als der relative Fehler (um Faktor 5 - 10)