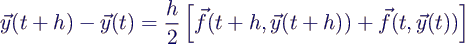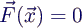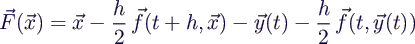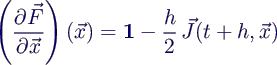Lösung von Aufgabe 22

• Alle Berechnungen können mit dem Matlab-Skript ex22.m ausgeführt werden.

• ode23t ohne Jacobimatrix
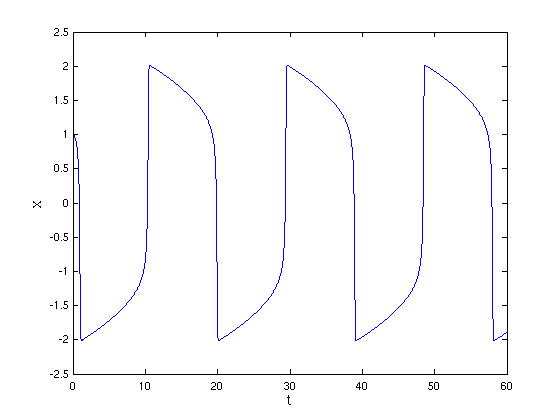
  • Zur Implementierung der Differentialgleichung wird zunächst die Systemfunktion f(t, y, mu) mit dem zusätzlichen Parameter mu definiert. In gewohnter Weise wird daraus die Funktion f1(t,y) abgeleitet. Um die Ergebnisse der drei Lösungen einfacher vergleichen zu können, wird dem Solver statt des Zeitintervalls [0 te] ein ganzer Vektor 0:h:te mit Ausgabezeitpunkten übergeben. Man erhält als Lösung
    • 
• ode23t mit Jacobimatrix
  • Die Jacobimatrix wird gemäß obiger Formel als Matrixfunktion J(t, y, mu) definiert, J1 hat den festen Parameterwert für mu. Mit Hilfe der Optionsstruktur
    • options = odeset("Jacobian", J1);
  • wird sie dem Solver mitgeteilt. Der Unterschied zu den Ergebnisse aus a. ist mit 3.8e-9 deutlich kleiner als die Genauigkeit des Solvers.
• mit eigenem Solver odeTrapez
  • Zur Lösung des nichtlinearen Gleichungssystems wird solveNewton.m verwendet.
  • Damit ausgerüstet kann das Trapezverfahren programmiert werden. Die nach y(t+h) aufzulösende Gleichung war ja
    • 
  • Nennt man zur Übersicht die gesuchte Größe in x um, kann man die Gleichung schreiben als
    • 
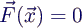
    • mit der Funktion
    • 
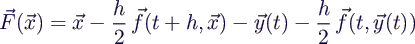
  • Die zugehörige Funktionalmatrix lässt sich bei bekannter Jacobimatrix J von f leicht berechnen, sie ist
    • 
  • Der Solver odeTrapez(f, tSpan, y0, h, J) benötigt neben den üblichen Argumenten noch eine feste Schrittweite h und die Funktion J(t,y) für die Jacobimatrix von f. Er definiert in jedem Zeitschritt die Hilfsfunktionen F und DF für das Newtonverfahren und bestimmt mit solveNewton den nächsten Wert von y. Alle Details findet man in odeTrapez.m .
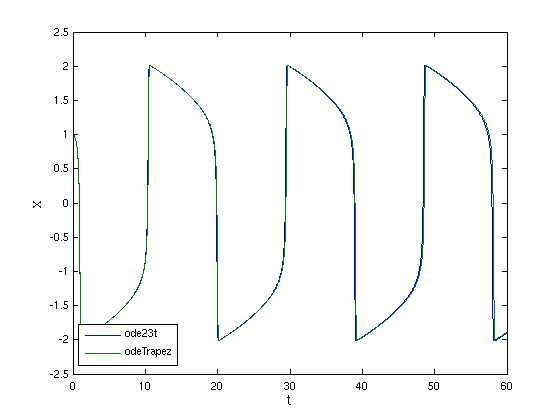
  • Plottet man die damit erhaltene Lösung, sieht man, dass die von odeTrapez erzeugte Lösung leicht hinterher hinkt
    • 
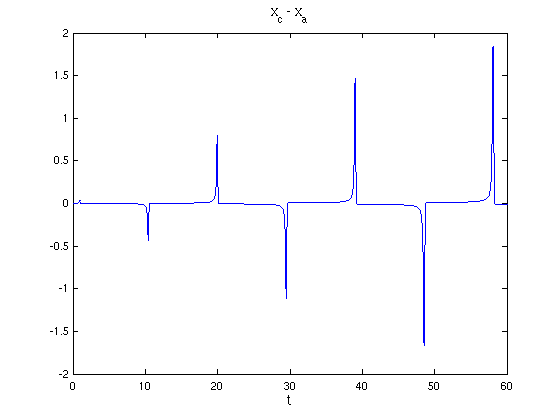
  • Die Abweichungen an den Sprungstellen werden dadurch zunehmend größer
    •