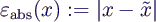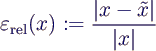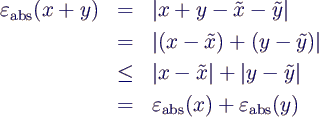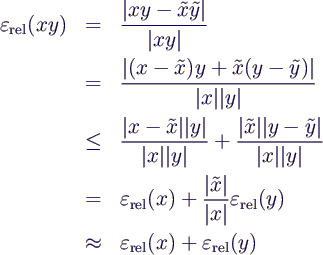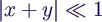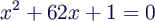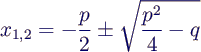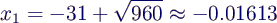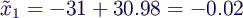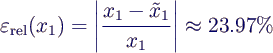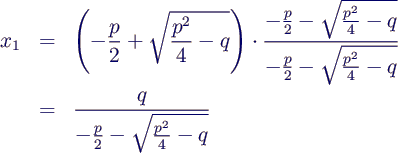Fehlerarten
- Numerische Mathematik:
- Entwicklung und theoretische Analyse von Verfahren
(Algorithmen) zur zahlenmäßigen Lösung mathematischer
Fragestellungen
- Ansprüche an Algorithmen
- endlich (selten) oder zumindest konvergent
(Normalfall)
- schnell = Zahl der Operationen (für eine
gewünschte Genauigkeit) möglichst klein
- stabil = ähnliche Ergebnisse bei kleinen
Störungen der Eingangsdaten
- Plot eines Polynoms mit
Matlab [1, S.42]:
- Beispiel-Polynom
- direkte Berechnung als Potenz (A) oder
ausmultipliziert (B) mit Matlab liefert
- wichtige Fehlerquellen:
- Abbruchfehler bei iterativen Verfahren
- Rundungsfehler durch ungenaue Darstellung der Zahlen
(Computer-Arithmetik)
- Datenfehler durch ungenaue Eingangswerte
- Fehlermaße:
- sei x ein genauer Wert,
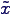 ein
Näherungswert
ein
Näherungswert
- absoluter Fehler
- relativer Fehler (für x ≠ 0)
- absoluter Fehler bei der Addition
- relativer Fehler bei der Multiplikation
- in vielen Anwendungen ist der relative Fehler
entscheidend!
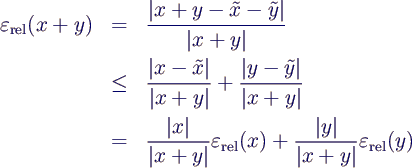
- Auslöschung:
- relativer Fehler bei der Addition
- problematisch für
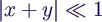
- also bei Subtraktion etwa gleich großer
Zahlen
- Lösung quadratischer Gleichungen:
- Beispiel
- Lösungsformel
- liefert als erste Lösung
- bei Rechnung mit 4 signifikanten Stellen aber
- mit einem relativen Fehler
- also: möglichst nie etwa gleich große Zahlen
subtrahieren!
- Alternativer Algorithmus:
- Lösungsformel umstellen
- Rechnung auf 4 signifikanten Stellen
- liefert also volle 4 signifikanten Stellen
Genauigkeit
- Kernthemen dieses Kurses:
- wichtige Algorithmen in Beispielen
- Sätze zu Konvergenz- und Stabilitätseigenschaften,
aber keine Beweise
- Implementierungen in Matlab



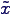 ein
Näherungswert
ein
Näherungswert