Statistische Analyse von Simulationsergebnissen
- Problemstellung:
- Modell mit stochastischen Prozessen
- → Simulationsergebnisse sind zufällig
- → Ergebnisse müssen statistisch analysiert werden
- Standardtests oft nicht anwendbar
- Ergebnisse zeitlich korreliert
- Verteilungen nicht stationär
- Nullhypothese "Modelldaten ≙ Systemdaten" ist
sicher falsch (bei hinreichender Genauigkeit)
- Standardbeispiel M|G|1-Queuing-System:
- Ankunftszeiten ~ Ex(λ)
- Servicezeiten ~ N(1/μ, σ2)
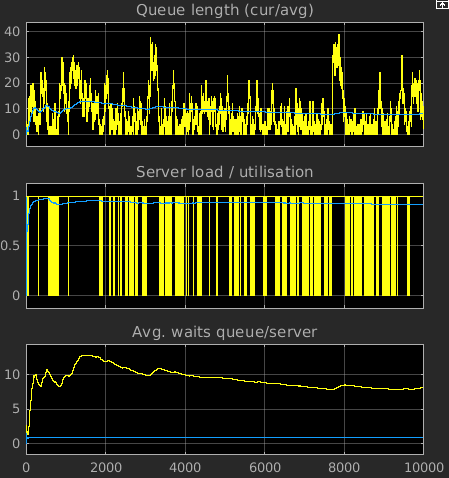
- Ausgaben
- aktuelle Queuelänge nQ(ti) mit Zeiten
ti
- mittlere Queuelänge LQ
- mittlere Wartezeit in der Queue WQ
- mittlere Serverauslastung A
- Beispiellauf mit Parametern λ = 1, μ = 1.2, σ = 0.9,
tEnd = 10000
- Ergebnisse von 6 Beispielläufen mit
aufeinanderfolgenden Seeds
-
| Lauf |
LQ |
WQ |
A |
| 1 |
8.0348 |
8.0814 |
0.9201 |
| 2 |
9.1228 |
9.0291 |
0.9287 |
| 3 |
7.3117 |
7.3779 |
0.9129 |
| 4 |
5.6341 |
5.8311 |
0.8785 |
| 5 |
10.2697 |
10.2059 |
0.9338 |
| 6 |
15.8034 |
15.5841 |
0.9428 |
- Abschätzen der mittleren Queuelänge - naiv (und falsch):
- betrachten Queuelänge Xi zu Zeiten ti
= i (i = 1 .. n)
- aus Modellergebnissen interpoliert (mit 'previous')
- mit üblichen Standardformeln aus den Xi berechnet
- Mittelwert LQ = 8.0380
- Varianz S2 = 61.5559
- zum Nachrechnen: tEnd = 10000, seed = 4
- Problem: LQ erscheint zu klein (angesichts
der Tabelle)
- Ursache: Korrelation der Werte innerhalb eines Laufs
- genauer: Korrelationskoeffizient ρ jeweils
aufeinanderfolgender Werte Xi und Xi+1
abschätzen
- Ergebnis
- ρ = 0.9859
- Werte sehr stark korreliert
- klar, z.B. Queue voll → aufeinander folgende Xi
alle groß
- Ensemblemittelung:
- k komplette Läufe mit verschiedenen Seeds
- → Daten Xij, i = 1..k, j = 1..n
- daraus Mittelwerte Yi pro Lauf bestimmen
- Gesamtmittel = Mittel über Läufe (Ensemblemittel)
- Yi sind i.i.d → Standardverfahren
funktionieren
- Schätzer für Varianz
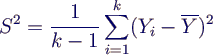
- Schätzer für (1-α)-Konfidenzintervall
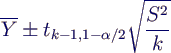
- Ensemblemittelung im Beispiel:
- k = 100 Läufe bis tEnd = 100 (statt tEnd
= 10000)
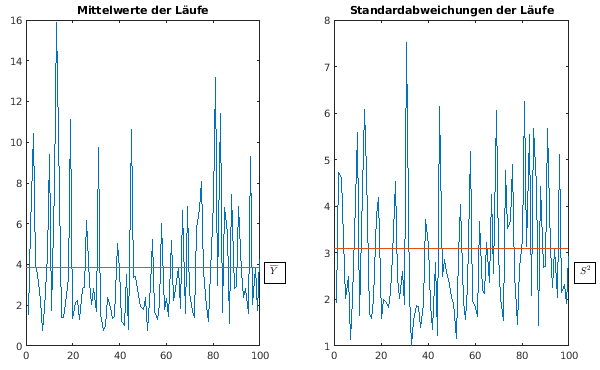
- Verteilung der Yi und der
Standardabweichungen pro Lauf
- Ergebnisse
 =
3.8414
=
3.8414- S2 = 9.5769
- Konfidenzintervall: [3.2274, 4.4554] für 1-α =
95%
- Ergebnis seltsam (vgl. Tabelle)
- Mittelwert anscheinend viel zu klein
- Konfidenzintervall enthält keins von 6
Ergebnissen
- Ursache
- Läufe zu kurz
- größere Queuelängen erst nach längerer Zeit
- Gleichgewicht (falls vorhanden) noch nicht
erreicht
- Abhilfe
- "Aufwärmzeit" abwarten, erst danach Werte nehmen
- Problem: Wie lange dauert die?
- Ermitteln der Aufwärmzeit tA:
- grundsätzlich
- häufig: Verteilungen für X(ti) haben
Limes für t→∞ (Steady State)
- gesucht: Laufzeit t, ab der Steady State ungefähr
erreicht ist
- schwierig, da Xi auch im Steady-State
stark schwanken
- graphisches Verfahren nach Welch [12]
- 1. mache k Läufe der Länge n → Daten Xij,
i = 1..k, j = 1..n
- 2. mittle Werte gleicher Zeit über die Läufe
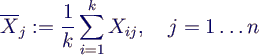
- verringert Varianz um k bei gleichem
Erwartungswert
- 3. mittle Werte über Zeitfenster der Breite w
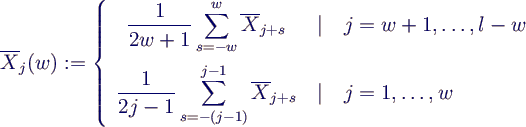
- glättet hochfrequente Anteile weg
- plotte
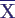 j(w)
für verschiedene w
j(w)
für verschiedene w
- wähle w so klein, dass Kurven "hinreichend glatt"
- im Zweifelsfall k vergrößern
- 4. plotte
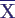 j(w)
und wähle tA, ab dem Grenzwert etwa erreicht
j(w)
und wähle tA, ab dem Grenzwert etwa erreicht
- Vorgehensweise im Beispiel (Replication/Deletion-Verfahren):
- Aufwärmzeit tA nach Welsh ermitteln
- k = 10 Läufe bis tEnd = 1000
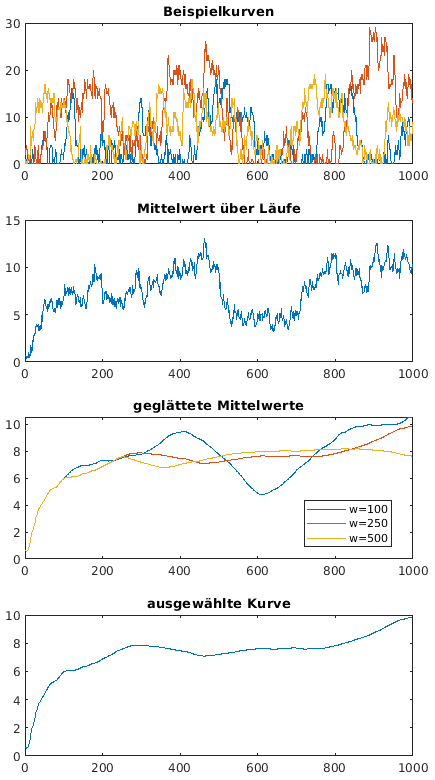
- geglättete Kurven mit w = 250 und w = 500 sehr
ähnlich
- Schwankungen bleiben groß
- Aufwärmbereich grob gut erkennbar
- wähle tA = 500 (eher etwas zu groß)
- Achtung Matlab
- gleitendes Mittel mit movmean
benutzt am Rand einseitige Intervalle
- damit wird der (entscheidende) Anstieg am Anfang
weggemittelt
- also: eigene Routine modmean2,
die korrekte Formel verwendet
- anschließend mit neuen Läufen Xij
bestimmen (Replication)
- jeweils Werte vor tA streichen (Deletion)
- mit den restlichen Werten Mittel Yi
über Läufe bestimmen
- Yi mit Standardverfahren auswerten
- Ergebnisse bei k = 10 und tEnd = 1500
 =
10.7314
=
10.7314- S2 = 56.1750
- Konfidenzintervall: [5.3698, 16.0930]
- gut verträglich mit Tabelle
- Ergebnisse bei k = 100 und tEnd = 1500
 = 9.4257
= 9.4257- S2 = 29.7782
- Konfidenzintervall: [8.3430, 10.5085]
- mehr Daten → deutlich höhere Genauigkeit
- Weitergehende Methoden:
- bisher nur an der Oberfläche gekratzt
- verschiedene Verfahren für endlichen (festen)
Zeitrahmen, Steady-State-Systeme oder steady-state-zyklische Systeme
- komplexe Methoden zum Vergleich zweier
Systemkonfigurationen
- ausgefeilte Verfahren zur Veringerung der Varianz
- guter Einstieg: [Law, Kap 9-11]
- Aufgaben:


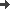
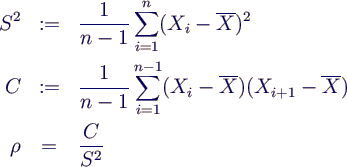
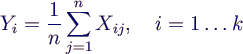
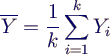
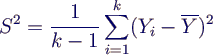
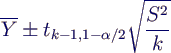
 =
3.8414
=
3.8414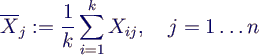
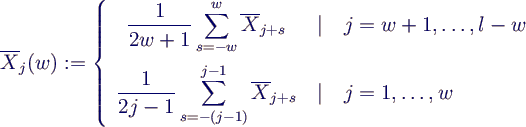
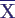 j(w)
für verschiedene w
j(w)
für verschiedene w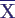 j(w)
und wähle tA, ab dem Grenzwert etwa erreicht
j(w)
und wähle tA, ab dem Grenzwert etwa erreicht
 =
10.7314
=
10.7314 = 9.4257
= 9.4257