Choosing the bins in the χ² test

• Experiment 1:
  • create rounded normal data
  • vary bin width and compute p-value
    • position of bins such that mean value is center of a bin
  • result
    • 
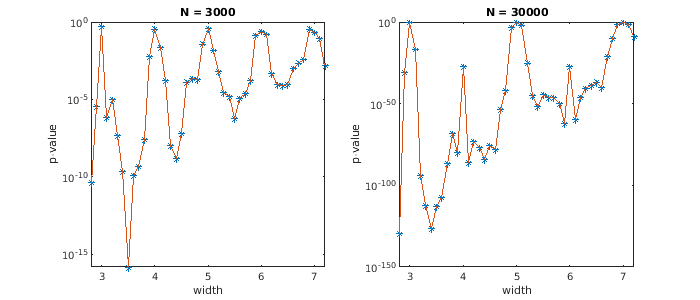
    • p-value large at integer widths
    • effect pronounced for odd width and large N
• Experiment 2:
  • use odd integer bin width (w = 5)
    • position edges initially at integers
    • shift positions
  • result
    • 
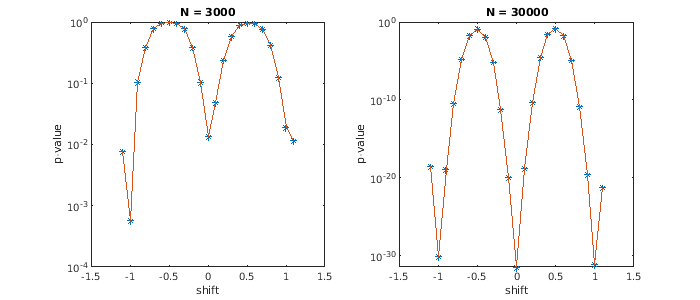
    • p-value minimal at integer shifts, maximal at half-integer shifts
• Explanation:
  • p-value is maximal for bins [n₁+0.5, n₂+0.5] (n₁,n₂ ∊ ℕ)
    • these bins are invariant under rounding
    • → expected bin counts identical with or without rounding
    • → χ² test can't detect rounding and confirms normal distribution
  • why odd width optimal in experiment 1?
    • mean value is (almost) 165
    • odd width → bin boundaries are on half-integers
• Suggestion:
  • use half-integer bin boundaries to get rid of rounding effects
  • easily adaptable to other measurement precisions
  • only works for χ² test