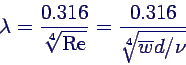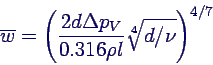Lösung von Aufgabe 12
- Bestimmung der Strömungsgeschwindigkeiten und Reynoldszahlen:
- Der Druckabfall bestimmt sich aus
- Δpv
= λ · l/d
· ρ/2 ·
 2
2
- Weiter gilt (vermutlich) die Formel von Blasius
- Setzt man dies oben ein und löst nach
 auf, erhält man
auf, erhält man
- Dies ergibt auf den beiden Teilstücken
-
 AB
= 0.969 m/s,
AB
= 0.969 m/s,  CD
= 0.439 m/s
CD
= 0.439 m/s
- Die Reynoldszahlen erhält man nun aus Re =
 d / ν zu
d / ν zu
- ReAB = 4.85 · 104, ReCD
= 2.19 · 104
- Beide Teilströmungen sind also turbulent und liegen im Gültigkeitsbereich
der Blasius-Beziehung.
- Die Volumenströme erhält man direkt aus
 = A
= A  =
=  π d2/4:
π d2/4:
 AB
= 1.90 · 10-3 m3/s
AB
= 1.90 · 10-3 m3/s -
 CD
= 0.862 · 10-3 m3/s
CD
= 0.862 · 10-3 m3/s
- ⇒
 Leck =
Leck =
 AB -
AB -  CD
= 1.04 · 10-3 m3/s
CD
= 1.04 · 10-3 m3/s
- Ort des Lecks:
- Der Druck fällt vor und hinter dem Leck linear ab. Dabei
ändert sich die Steigung des Abfalls am Leck:
- Der Ort des Lecks ist der Schnittpunkt der beiden Geraden
I und II. Mit den Bezeichnungen
-
 = p / bar,
= p / bar, 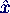 =
x / km
=
x / km
- lauten diese
- I:
 = -2
= -2 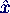 + 6
+ 6
- II:
 = -0.5
= -0.5 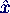 + 2.75
+ 2.75
- Der Schnittpunkt
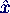 L
ergibt sich durch Gleichsetzen der Geradengleichungen zu
L
ergibt sich durch Gleichsetzen der Geradengleichungen zu
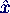 L
= 2.1667
L
= 2.1667
- Das Leck befindet sich also 1167 m hinter Punkt B.
 2
2  auf, erhält man
auf, erhält man
 AB
= 0.969 m/s,
AB
= 0.969 m/s,  CD
= 0.439 m/s
CD
= 0.439 m/s  d / ν zu
d / ν zu
 AB
= 1.90 · 10-3 m3/s
AB
= 1.90 · 10-3 m3/s  CD
= 0.862 · 10-3 m3/s
CD
= 0.862 · 10-3 m3/s  Leck =
Leck =
 AB -
AB -  CD
= 1.04 · 10-3 m3/s
CD
= 1.04 · 10-3 m3/s 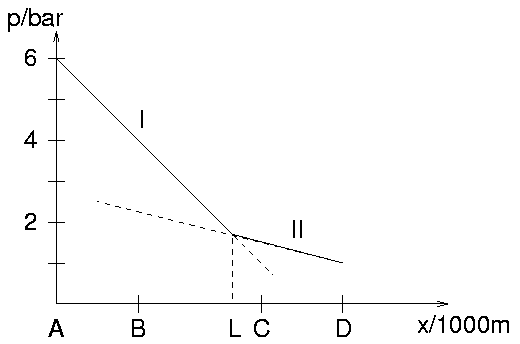
 = p / bar,
= p / bar, 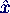 =
x / km
=
x / km  = -2
= -2 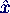 + 6
+ 6  = -0.5
= -0.5 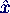 + 2.75
+ 2.75
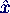 L
ergibt sich durch Gleichsetzen der Geradengleichungen zu
L
ergibt sich durch Gleichsetzen der Geradengleichungen zu
 L
= 2.1667
L
= 2.1667