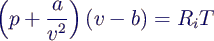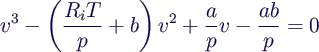Zustandsgleichungen realer Gase

• Abweichung vom idealen Gas:
  • Realgasfaktor
    • Z := p v / (R_i T)
  • als Funktion von p und T für Stickstoff
    
• Van-der-Waals-Gleichung:
  • erweitert ideale Gasgleichung um zwei Korrekturterme
    • Anziehungskräfte zwischen Molekülen → Druckkorrektur
    • Eigenvolumen der Moleküle → Volumenkorrektur
  • Damit
    • 
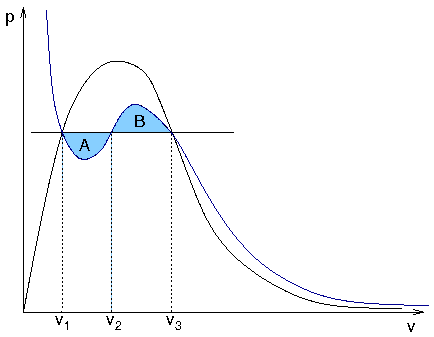
  • im p-V-Diagramm
    
  • geschrieben als Gleichung für v
    • 
  • für kleine Werte von p
    • drei Lösungen (v₁,v₂, v₃ im Bild)
    • Kurve unphysikalisch
    • Flüssigkeit nicht berücksichtigt
    • Ersetzen durch gerade Linie, so dass Flächen A und B gleich groß
  • für große Werte von p
    • eine Lösung
    • Grenzfall am kritischen Punkt
    • kritische Temperatur: Wendepunkt mit waagerechter Tangente
    • damit:
    • a = 3 p_k v_k²
    • b = v_k/3
    • R_i = 8 p_k v_k / (3 T_k)
• Virialgleichung:
  • empirischer Ansatz
    • p = R_iT/v + B(T)/v² + C(T)/v³ + D(T)/v⁴ + ...
  • B, C, D: Virialkoeffizienten
  • viele andere Gleichungen zur näherungsweisen Beschreibung realer Gase
  • in der Praxis: Messwerte als Tabellen oder Computerprogramme
• Aufgaben:
  • Aufgabe 12