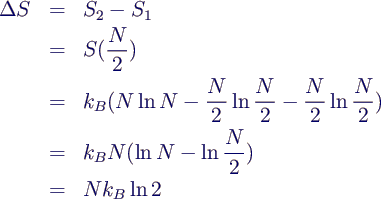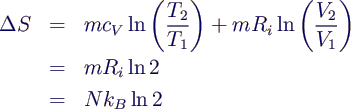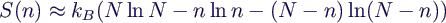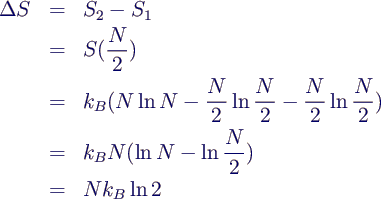Entropie und statistische Physik

• Entropie in der statistischen Mechanik (vgl. Physik 2):
  • definiert über die Zahl W möglicher Zustände, die den gleichen makroskopischen Zustand beschreiben
    • S_mikro := k_B ln W
  • Maß für die Ordnung eines Systems (hohe Ordnung → S klein)
• Erklärung des 2. Hauptsatzes aus der statistischen Mechanik:
  • Zahl der Zustände mit höherer Entropie bedeutend größer als mit kleinerer Entropie
  • Übergang zu kleinerer Entropie nicht verboten, aber extrem unwahrscheinlich
  • Kartenspiel als Beispiel:
    • am Anfang geordnet (niedrige Entropie)
    • Mischen → Unordnung steigt (Entropie wächst)
    • spontanes Sortieren durch Mischen extrem unwahrscheinlich
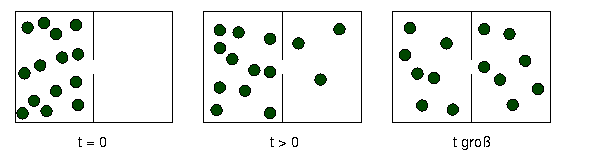
  • ausströmendes Gas
    
    • Teilchen verteilen sich über ganzes Volumen
    • spontane Sammlung auf einer Seite grundsätzlich möglich
    • sehr unwahrscheinlich
    • bei großen Teilchenzahlen (~ 10²²) extrem unwahrscheinlich
    • tritt praktisch nie auf
• Beispiel: adiabate Expansion des idealen Gases
  • ideales Gas dehne sich adiabatisch und isotherm in ein Vakuum auf doppeltes Volumen aus
  • Entropie klassisch
    • 
  • Entropie statistisch
    • Entropie bei n Teilchen im linken Teilvolumen
    • 
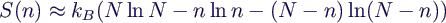
    • am Anfang n = N, also W = 1, somit S₁ = 0
    • am Ende n = N/2, daher
    •