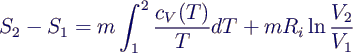Definition der Entropie

• Entropie differentiell:
  • für reversible Prozesse gegeben als Wärmeänderung pro Temperatur
    • dS := dQ/T    (reversibel)
  • bei nicht-reversiblen Prozessen wird Dissipationswärme berücksichtigt
    • dS := (dQ + dW_diss)/T
  • mit 1. Haupsatz:

    dU	= dQ + dWdiss - p dV
    	= T dS - p dV
    ⇒ dS	= (dU + p dV)/T

• Entropie beim idealen Gas:
  • kalorische Zustandsgleichung
    • dU = m c_V dT
  • thermische Zustandsgleichung
    • p = m R_i T / V
  • damit
    • dS = m c_V dT/T + m R_i dV/V
  • lässt sich integrieren zu
    • 
  • hängt nicht vom Weg, sondern nur von Anfangs- und Endzustand ab
  • für konstantes c_V
    • S₂ - S₁ = m c_V ln(T₂/T₁) + m R_i ln(V₂/V₁)
  • analog über dH:
    • S₂ - S₁ = m c_p ln(T₂/T₁) - m R_i ln(p₂/p₁)
• Grundlegende Eigenschaft der Entropie:
  • Entropie ist Zustandsgröße, d.h. hängt nicht vom Prozessverlauf ab
  • gilt grundsätzlich (nicht nur beim idealen Gas)
  • Erfahrungstatsache (Ergebnis von Experimenten)
  • mathematisch begründbar, aber schwierig