Kalorische Zustandsgleichung
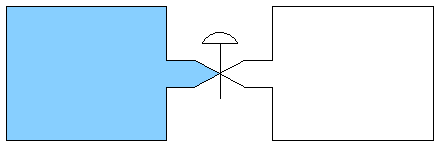
- Überströmversuch:
- (ideales) Gas expandiert in ein Vakuum hinein:
- Beobachtung: Nach Ausgleich anfänglicher Temperaturunterschiede
ist die Endtemperatur gleich der Anfangstemperatur.
- Interpretation mit Hilfe der kalorischen Zustandsgleichung
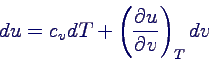
- du = 0, denn dQ = 0 und dWV = 0 (wegen p
= 0)
- dT = 0 nach Beobachtung
- → u hängt nicht von v ab
- Kalorische Zustandsgleichung des idealen Gases:
- Innere Energie hängt nicht vom (spezifischen) Volumen
ab, also:
- integriert:
- (letzteres nach Definition des Durchschnittswerts)
- für die spezifische Enthalpie ergibt sich:
- hängt also auch nur von der Temperatur ab, nicht vom Druck
- kalorische Zustandsgleichung für die Enthalpie:
- integrierte Form analog zu u.
- Beziehung zwischen cp und cv:
- Aus h = u + Ri T folgt:
- dh - du = Ri dT
⇒ cp dT - cV dT = Ri
dT
⇒ cp - cV = Ri
- Die Differenz der spezifischen Wärmen beim idealen Gas
ist unabhängig von der Temperatur.
- Adiabatenkoeffizient κ:
- definiert durch:
- cv steigt in der Regel mit T, κ sinkt
dementsprechend.
- nützliche Beziehung zwischen h und u beim idealen Gas:
- dh = cp dT = κ cv dT =
κ du
- Molare Wärmekapazität:
- Cm,p und Cm,v: auf ein Mol bezogen,
d.h. mit der Molmasse M:
- Differenz beider Größen:
- Cm,p - Cm,v = M (cp
- cV) = M Ri = R
- Die Differenz der molaren Wärmekapazitäten beim idealen
Gas ist unabhängig von der Temperatur und von der Stoffart.
- Aus der Differenz und dem Verhältnis Cm,p /
Cm,v = κ kann man beide Größen auf κ zurückführen:
- Folgerung aus der statistischen Mechanik:
- innere Energie bei insgesamt f Freiheitsgraden
- Folgerung beim einatomigen Gas:
- 3 Translationsfreiheitsgrade (Bewegung in 3 Raumrichtungen)
- f = 3
- κ = 5/3
- cv = 3/2 Ri
- cv ist temperatur-unabhängig (perfektes Gas)
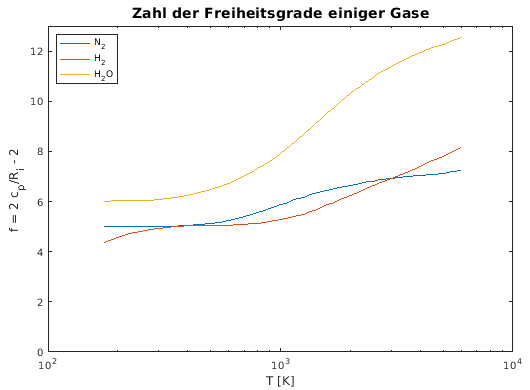
- Folgerung beim zweiatomigen Gas:
- Zahl der Freiheitsgrade f:
- 3 Translationsfreiheitsgrade
- 2 Rotationsfreiheitsgrade (Achsen senkrecht zur Hantel)
- 2 Schwingungsfreiheitsgrade (für eine
Schwingungsform)
- Rotationen brauchen bestimmte Mindestenergien
(Quantenmechanik!), daher erst bei mittleren Temperaturen (> 100
... 200 K) wirksam
- Drehung um Hantelachse braucht sehr hohe
Anregungs-Energie
 2/J, da das Trägheitsmoment sehr niedrig
2/J, da das Trägheitsmoment sehr niedrig
- Schwingungen brauchen noch höhere Energien, sind daher
typischerweise erst ab T > 1000K aktiv
- f, cv und κ also
temperaturabhängig
- Verhältnisse beim mehratomigen Gas:
- viele verschiedene Rotations- und Schwingungsfreiheitsgrade
- komplizierte Temperaturabhängigkeit von f und cv
- reale Werte für die "Zahl der Freiheitsgrade"
aus Messung von cp:
- Aufgaben:



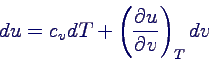
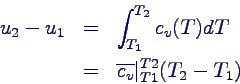
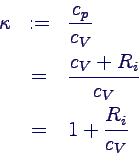
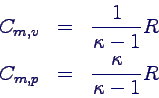
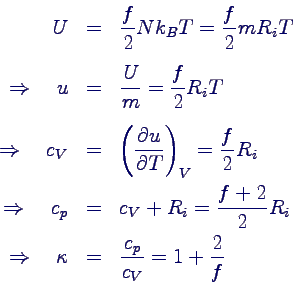
 2/J, da das Trägheitsmoment sehr niedrig
2/J, da das Trägheitsmoment sehr niedrig