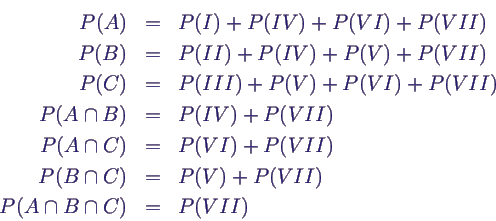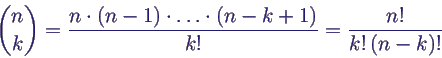Definition der Wahrscheinlichkeit
- Beispiel "idealer Würfel":
- Ergebnisse eines Wurfs: {1, 2, 3, 4, 5, 6}
- Ereignisse
- E1: Es wird eine 6 gewürfelt
- E2: Es wird eine Zahl < 3
gewürfelt
- E3: Es wird eine ungerade Zahl
gewürfelt
- Elementarereignis: Ereignis,
das nur aus einem einzigen Ergebnis besteht
- Annahme: Ergebnisse gleichwahrscheinlich, also
- P({1}) = ... = P({6}) = 1/6
- Wahrscheinlichkeit eines Ereignisses durch
Abzählen der enthaltenen Elementarereignisse
- P(E1) = P({6}) = 1/6
- P(E2) = P({1,2}) = 2/6
- P(E3) = P({1,3,5}) = 3/6
- Beispiel "Drehen eines Glücksrads":
- kreisförmige Scheibe mit Sektor-Markierungen
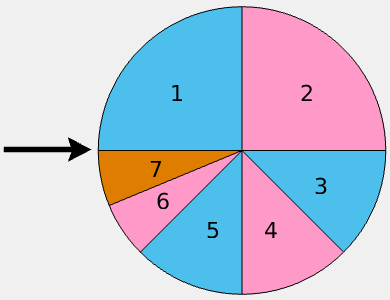
- wird kräftig in Drehung versetzt und kommt
durch Reibung zum Stehen
- feststehender Pfeil zeigt auf die Scheibe und
definiert das Ergebnis
- Ergebnisse: jeder beliebige Winkel φ ∈ [0,
360°)
- Ereignisse
- E1: der Winkel beträgt 90°
- E2: der Winkel liegt zwischen 45°
und 90°
- E3: der Sektor "7" wird erreicht
- E4: ein roter Sektor wird erreicht
- Annahme: alle Ergebnisse gleichwahrscheinlich
- unendlich viele Ergebnisse, sogar
überabzahlbar viele!
- P(E1) = P({φ, beliebig}) = 0
- Wahrscheinlichkeit eines Ereignisses =
eingeschlossene Fläche / Kreisfläche
- P(E2) = 1/8
- P(E3) = 1/16
- P(E4) = 1/4 + 1/8 + 1/16 = 7/16
- Definition des Wahrscheinlichkeitsraums (Ω, ℱ,
P):
- Menge Ω (Ergebnisraum)
- Menge ℱ von Teilmengen von Ω (Ereignisraum)
mit folgenden Eigenschaften (σ-Algebra)
- Abbildung P: ℱ → [0,1] (Wahrscheinlichkeitsmaß)
mit
- Anmerkung zu ℱ:
- bei endlichem oder abzählbarem Ω oft
einfach
- ℱ =
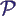 (Ω)
(Potenzmenge von Ω)
(Ω)
(Potenzmenge von Ω)
- bei überabzahlbarem Ω (z.B. Intervall
reeller Zahlen)
- Potenzmenge "zu groß" → keine
sinnvolle Definition von P möglich
- Ausweg: nur "vernünftige" Teilmengen
zulassen
- bei reellen Zahlen z.B. Intervalle und ihre
abzählbaren Durchschnitte und Vereinigungen
- i. F. wird ℱ immer so angenommen
- Einfache Folgerungen:
- P(Ac) = 1 - P(A)
- P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
- A ⊂ B ⇒ P(B \ A) = P(B) - P(A)
- P(B \ A) = P(B) - P(A ∩ B)
- P(A ∪ B ∪ C) = P(A) + P(B) + P(C) -
P(A ∩ B) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B
∩ C)
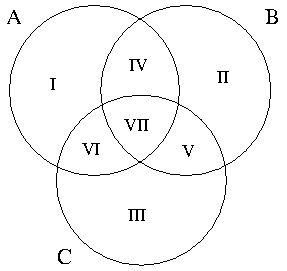
- Beweis von 5:
- Ereignisse als Flächen symbolisiert
- Zerlegung in disjunkte Teile liefert sofort
- Einsetzen in (5) ergibt dann
- P(A ∪ B ∪ C) = P(I) + P(II) + P(III)
+ P(IV) + P(V) + P(VI) + P(VII)
- Beispiel n-faches Würfeln:
- Ω = {(a1,a2, .., an)
| ai ∈ {1,2,3,4,5,6} }
- P(ω) = 1/6n für alle ω
∈ Ω
- Wie groß ist die Wahrscheinlichkeit, beim
Mensch-ärger-dich-nicht herauszukommen?
- konkret: A = bei dreimaligem Würfeln
mindestens eine 6 würfeln
- Trick: Berechnung des Gegenereignisses
- Ac = bei dreimaligem Würfeln
keine 6 würfeln
- P(Ac) = 53/63
- P(A) = 1 - P(Ac) = 1 - 53/63
= 42.13 %
- Laplace-Experiment:
- Ω endlich
- Annahme: alle Elementarereignisse
gleichwahrscheinlich
- Wahrscheinlichkeit eines Ereignisses durch
Abzählen der enthaltenen Elementarereignisse
- Kombinatorik nützlich
- Zahl der Permutationen (Vertauschungen) von n
Elementen
- P(n) = n! = 1 · 2 · ... · n
- Zahl der Möglichkeiten, k Elemente von n
auszuwählen
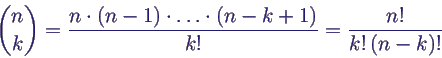
- Beispiel Kniffel:
- berechne P(FullHouse) beim Kniffel
- Anzahl von FullHouse-Ergebnissen, sortiert: XXXYY,
6*5 Möglichkeiten
- Anzahl verschiedener Reihenfolgen
- generell: 5! = 120
- Vertauschen der X bzw. Y untereinander liefert
keine neuen Reihenfolgen!
- es bleiben: 5!/(3! 2!) = 120/(6*2) = 10
- Damit
- |A| = 10*30 = 300
- |Ω| = 6^5 = 7776
- ⇒ P(A) = 300/7776 = 3.858 %
- Aufgaben:




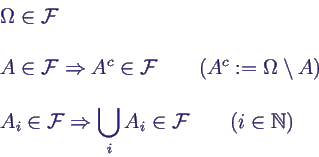
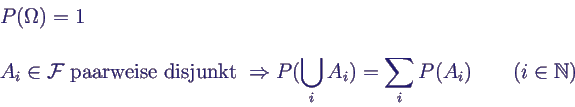
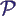 (Ω)
(Potenzmenge von Ω)
(Ω)
(Potenzmenge von Ω)