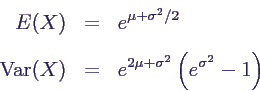Aufgabe 14

• Eine Zufallsvariable X heißt logarithmisch normalverteilt (mit Parametern μ und σ²), kurz: X ~ LN(μ, σ²), wenn ihr Logarithmus normalverteilt ist (mit Parametern μ und σ²), also wenn
  • X = exp(Y) mit Y ~ N(μ, σ²)
• Sie findet Anwendung z. B. zur Beschreibung von Aktienkursen im Black-Scholes-Modell.
• a. Berechnen Sie die Wahrscheinlichkeitsdichte von X
• b(*) Beweisen Sie folgende Formeln für Mittelwert und Varianz von X:
  • 
• Der Kurs X einer Aktie zu verschiedenen Tagen gehorche einer logarithmischen Normalverteilung mit E(X) = 10 € und σ(X) = 2 €.
• c. Plotten Sie die Wahrscheinlichkeitsdichte und Verteilungsfunktion von X.
• d. Wie groß ist der Median von X?
• e. Wie groß ist die Wahrscheinlichkeit, dass der Wert der Aktie auf über 12 € steigt?
• Achtung: Dieses Modell ist voller (unrealistischer) Annahmen - damit sollte man nicht an der Börse spekulieren!