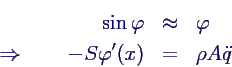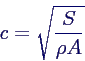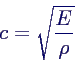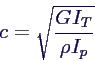Die Wellengleichung

• Eindimensionale kontinuierliche Schwinger:
  • kontinuierliche Verteilung von
    • Trägheitselementen (Masse, Trägheitsmoment)
    • Rückstellkräften
    • ggf. Dämpfung
  • i.f. nur eindimensional (z.B. Stäbe, Balken)
  • Dämpfung wird vernachlässigt
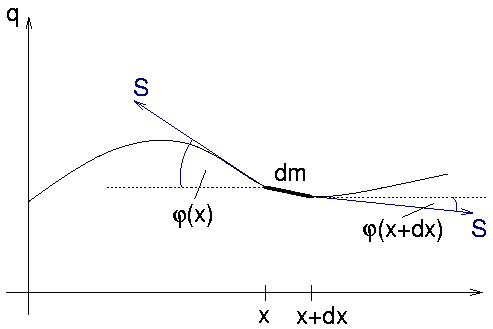
• Saite:
  • biegsam, erst durch Vorspannung S schwingfähig
  • Anwendungen
    • Spannseile
    • Treibriemen
    • Überlandleitungen
  • betrachten kleine Auslenkungen q(x, t)
    • nur in einer Ebene
    • Spannkraft S näherungsweise konstant
  • Kräfte auf Massenelement dm
    
  • Kräftebilanz senkrecht zur Auslenkung (in q-Richtung)
    • 
  • Masse bei konstantem Querschnitt A und Dichte ρ
    • dm = ρ A dx
  • kleine Auslenkungen →
    • 
  • φ ist negativer Winkel der Tangente, also
    • 
  • zusammengefasst folgt
    • 
• Grundform der Wellengleichung:
  • mit Parameter c (Ausbreitungsgeschwindigkeit)
    • 
  • Bewegungsgleichung der Saite mit
    • 
  • partielle Differentialgleichung für q(x,t)
  • analog bei Längsschwingungen eines Stabs mit Kompressionsmodul E mit
    • 
  • ebenso für Torsionsschwingungen einer Welle mit Torsionssteifigkeit G I_T und polarem Flächenmoment 2. Grades I_p
    • 
  • bei kreis- oder kreisringförmigem Querschnitt ist I_T = I_p