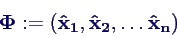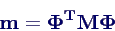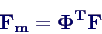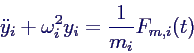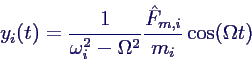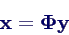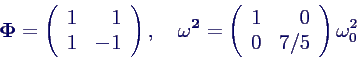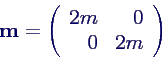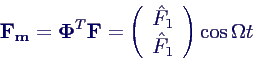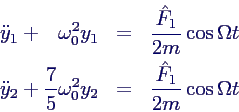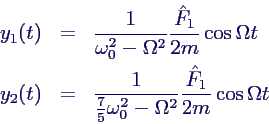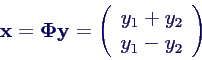Lösung durch Modaltransformation

• Vorgehensweise:
  • Bestimmung der Eigenfrequenzen ω_i und Eigenschwingungen 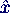_i des homogenen Systems
  • Aufstellen der Modalmatrix Φ
    • 
  • Berechnen der Massenelemente m_i aus
    • 
  • Bestimmung der modalen Anregungen
    • 
  • entkoppelte Gleichungen in Hauptkoordinaten lauten damit
    • 
  • Lösungen für Hauptkoordinaten y_i wie im 1d-Fall ohne Dämpfung
    • 
  • Lösung in Ausgangskoordinaten durch Rücktransformation
    • 
• Anwendung im Standardbeispiel:
  • Eigenfrequenzen und Modalmatrix
    • 
  • Massenelemente
    • 
  • modale Anregungen
    • 
  • entkoppelte Gleichungen in Hauptkoordinaten
    • 
  • Lösung für die y_i
    • 
  • Rücktransformation auf Ausgangskoordinaten
    • 
  • Einsetzen ergibt
    • 
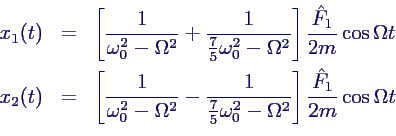
    • in Übereinstimmung mit dem früheren Ergebnis
• Modale Erregerkraft F_m,i:
  • regt i-te Eigenschwingung an
  • Anteil der Kraft in Richtung des Eigenvektors 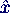_i (Skalarprodukt)
  • F_m,i = 0 →
    • Kraft steht senkrecht auf Eigenschwingung
    • Eigenschwingung wird nicht angeregt
• Aufgaben:
  • Aufgabe 13
  • Aufgabe 14