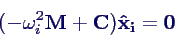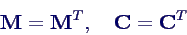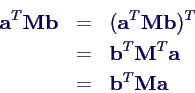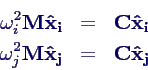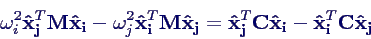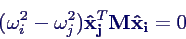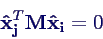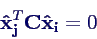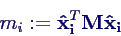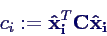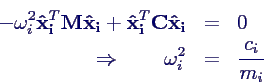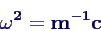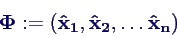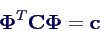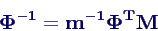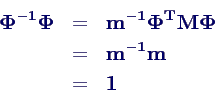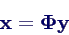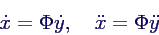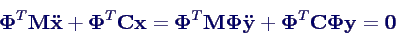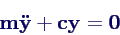Herleitung der Modaltransformation

• Grundlegende Beziehungen
  • Nach Definition der Eigenvektoren 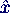_i gilt die Eigenwertgleichung
    • 
  • Matrizen M und C sind symmetrisch
    • 
  • daher folgt für beliebige Vektoren a und b
    • 
  • analog für C
• Orthogonalität der Eigenvektoren
  • Für zwei Eigenvektoren 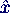_i, 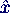_j (i ≠ j) zu verschiedenen Eigenfrequenzen gilt
    • 
  • Multiplizieren der 1. Gleichung mit 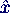_j^T, der zweiten mit 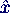_i^T und Subtraktion →
    • 
  • Symmetrie von M und C liefert
    • 
  • wegen ω_i ≠ ω_j folgt also
    • 
  • dies oben eingesetzt ergibt sofort
    • 
  • im folgenden nehmen wir immer an, dass alle Eigenfrequenzen verschieden sind.
• Normierung der Eigenvektoren
  • modale Massen m_i sind definiert durch
    • 
  • modale Steifigkeiten c_i durch
    • 
  • Multiplikation der Eigenwertgleichung mi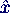t _i^T ergibt
    • 
  • oder in Matrixform mit den Diagonalmatrizen m = diag(m_i) etc.
    • 
• Eigenschaften der Modalmatrix
  • definiert als Matrix der Eigenvektoren
    • 
  • Betrachte Elemente der Matrix Φ^T M Φ
    • 
  • analog erhält man
    • 
  • Die Inverse Φ^-1 der Modalmatrix berechnet man als
    • 
  • es ist nämlich
    • 
• Übergang zu Hauptkoordinaten
  • Definition der Hauptkoordinaten y durch
    • 
  • Ableitung der Matrixmultiplikation ergibt
    • 
  • Einsetzen in Bewegungsgleichung und Multiplikation mit Φ^T →
    • 
  • mit den obigen Beziehungen daher
    • 
  • m und c sind Diagonalmatrizen, d.h. die Gleichungen lauten in Koordinaten
    •