Klänge

• Erzeugen eines Klangs:
  • Berechnen eines Sinustons vorgegebener Frequenz, Amplitude und Dauer mit createSineWave
  • hier immer mit fester Samplefrequenz 44.1 kHz
  • Beispiel
    • f = 200;
      A = 0.3;
      T = 2;
      [y1, t] = createSineWave(f, A, T);
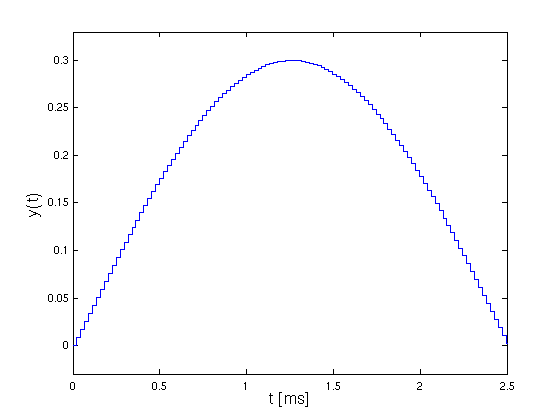
  • Plot der Schwingung
    • 
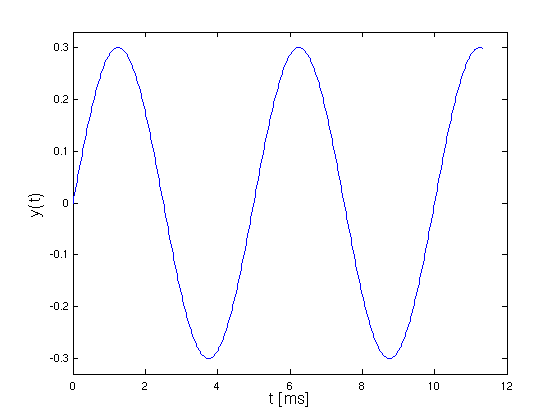
    • Vergrößerung zeigt die Diskretisierung (mit Plotfunktion stairs)
    • 
  • abspielen mit
    • sound(y1, 44100)
  • Wertebereich für Sounds in Matlab: [-1, 1] (für double-Werte)
  • Klang verändern durch Hinzufügen von Obertönen
    • y2 = createSineWave(2*f, A/2, T);
      y3 = createSineWave(3*f, A/3, T);
      y4 = createSineWave(4*f, A/4, T);
      y5 = createSineWave(5*f, A/5, T);
      y6 = createSineWave(6*f, A/6, T);
      y = y1 + y2 + y3 + y4 + y5 + y6;
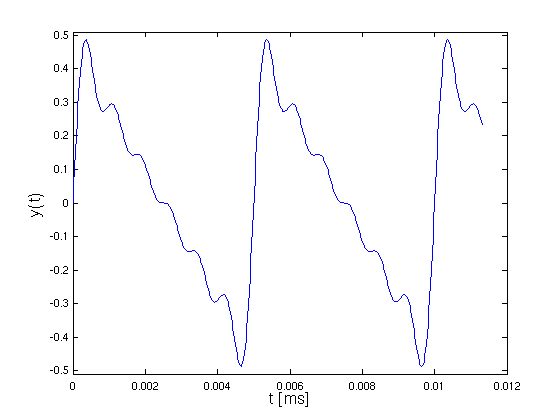
  • Schwingungsform nahezu sägezahnförmig
    • 
  • Klang "schärfer" (obertonreicher) als beim Sinus
  • abspeichern als Wave-Datei
    • audiowrite("ton.mp3", y, 44100)
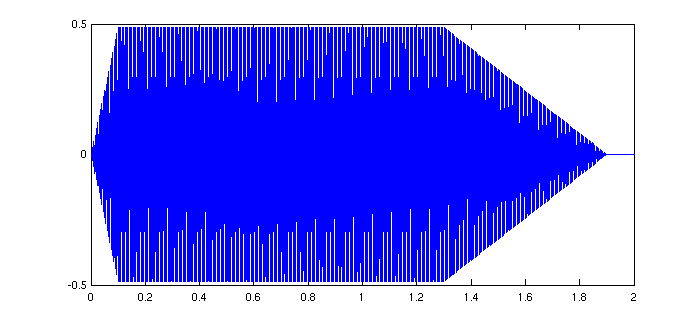
• Verändern des zeitlichen Lautstärke-Verlaufs:
  • typische Hüllkurve
    • steigt von 0 auf 1 an (Attack-Phase)
    • bleibt auf festem Wert (Sustain-Phase)
    • klingt wieder auf 0 ab (Release-Phase)
    • 
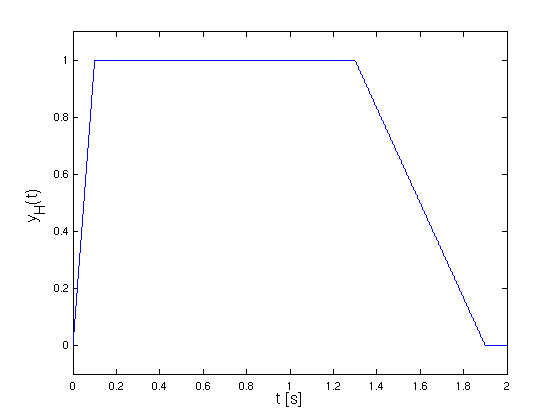
  • erzeugen mit Funktion createEnvelope
  • Ton mit Hüllkurve versehen und abspeichern
    • yEnv = createEnvelope(0.1, 1.2, 0.6, T);
      yH = yEnv.*y;
      audiowrite("ton1.mp3",yH,44100)
  • Ergebnis ton1.mp3
    • 
• Analyse eines Tons:
  • Laden von ton2.mp3
    • [y, Fs] = audioread("ton2.mp3");
    • Fs = 44100 (Samplerate)
  • Eigenschaften von y
    • Array von 588672x2 double-Werten
    • 2 Kanäle (Stereo)
    • Länge 588672/44100 = 13.3486 s
    • 
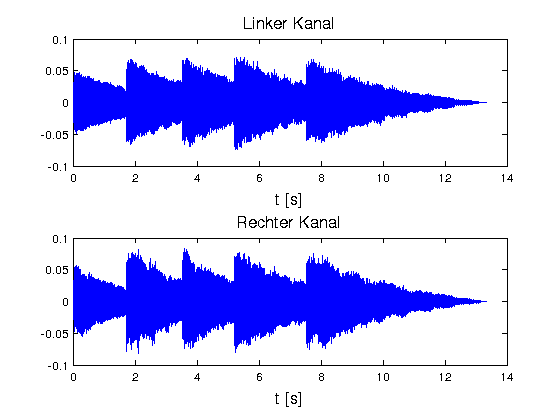
  • in Mono verwandeln
    • yMono = (y(:,1) + y(:,2))/2;
  • 1. Ton herausgreifen
    • Anzahl der Sample aus dem Bild abgeschätzt und für das Folgende auf Zweierpotenz abgerundet
    • N1 = 73400;
      N = 2^16
      y1 = yMono(1:N);
  • Spektralanalyse
    • bestimmt Aufbau eines Signals aus Grund- und Obertönen
    • grundlegendes mathematisches Verfahren: Fourieranalyse
    • in Matlab als Funktion fft(y)
    • deutlich schneller, wenn length(y) Zweierpotenz
  • Hilfsfunktion spektrum
    • berechnet das Spektrum Y der Werte y
    • gibt außerdem die passenden Frequenzwerte zurück
    • Samplerate als Parameter
  • Eigenschaften des Spektrums
    • größte erlaubte Frequenz: f_max = F_S/2
    • Frequenzauflösung (Frequenz-Schrittweite von Y) Δf = 1/T
  • im Beispiel
    • [Y, f] = spektrum(y1, 44100);
      plot(f, Y)
    • 
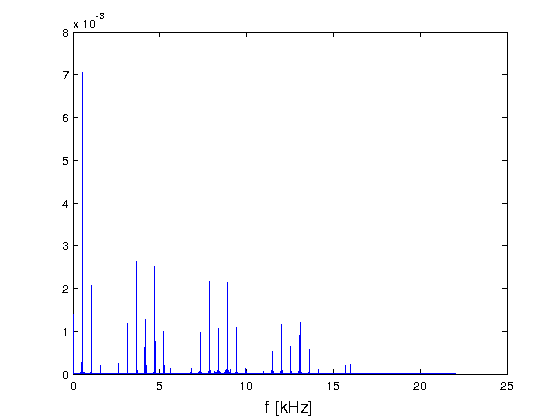
    • Ausschnitt
    • 
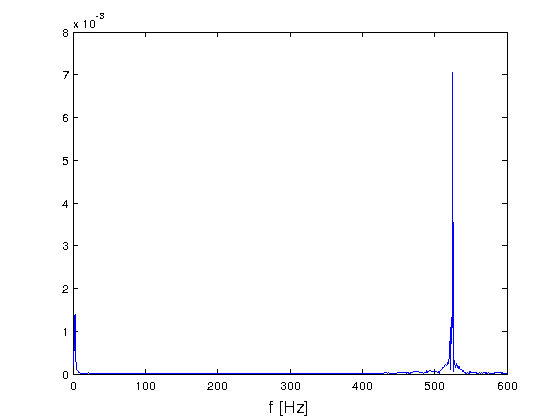
  • Bedeutung
    • Grundton bei 525 Hz (Ton: c²)
    • viele Obertöne bei ganzzahligen Vielfachen
    • niederfrequente Schwingung bei etwa 3 Hz (Vibrato)
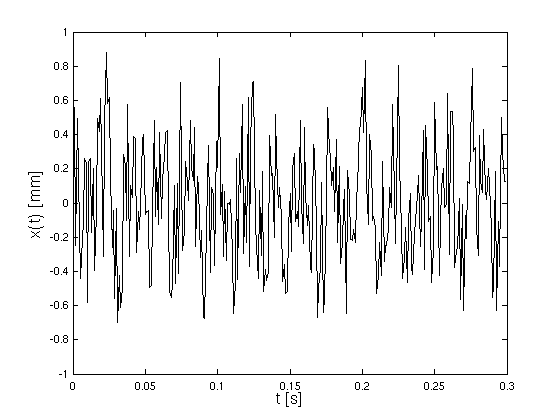
• Analyse einer Schwingung:
  • Störschwingungen einer Maschine werden in festen Zeitabständen aufgezeichnet
    • 
    • und abgespeichert (stoerung.dat)
  • in Matlab laden
    • xx = load("stoerung.dat");
      t = xx(:,1);
      y = xx(:,2);
    • und Samplefrequenz bestimmen
    • dt = t(2) - t(1); % sollten alle gleich sein
      Fs = 1/dt
  • FFT-Analyse mit
    • [Y, f] = spektrum(y, Fs);
  • Ergebnis:
    • 
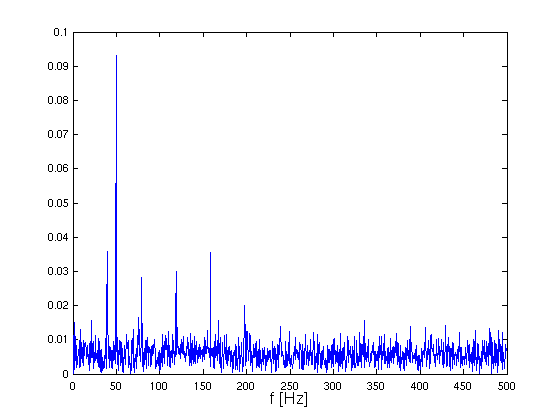
    • große Spitze bei 50 Hz
    • Spitzen in festen Frequenzabständen (Grundfrequenz 39.6 Hz)
    • Untergrund bei allen Frequenzen
  • Interpretation
    • Rauschen (Messfehler + allgemeine Störungen) als Untergrund
    • Trafoschwingungen bei 50 Hz
    • Störung mit Grundfrequenz 39.6 Hz und starken Oberfrequenzen (d. h. schnellen Änderungen, etwa Stöße)